Stage expérimental de Licence 3 : Instabilité de Faraday - Diffusion d'une onde acoustique sur l'interface liquide-air (Juillet 2013)
Dans le cadre du stage court expérimental de Licence 3 de Physique de l'Ecole Normale Supérieure, j'ai réalisé mon stage au Laboratoire de Physique Statistique. Le but était de comparer l'évolution de l'instabilité de Faraday avec l'accélération de la cuve par une mesure acoustique sur l'interface air/liquide et par une mesure capacitive classique.
Sommaire
 FIG 1 - Instabilité de Faraday
FIG 1 - Instabilité de Faraday
Sujet du stage
Des ondes de surface peuvent être engendrées à l'interface liquide-air d'un fluide soumis à une vibration verticale (instabilité de Faraday). Les ondes sont stationnaires (en général à la fréquence moitié de celle de la vibration) au seuil de l’instabilité. A amplitude de vibration plus élevée, elles deviennent désordonnées et fournissent un exemple canonique de système dynamique présentant des régimes de chaos spatio-temporel. Le stage consiste à mettre au point une nouvelle méthode de mesure, basée sur la diffusion d’une onde acoustique par l’interface liquide-air, afin d’étudier ces phénomènes. Dans un premier temps , les caractéristiques de l'instabilité de Faraday seront abordées dans ce rapport puis dans un second temps la transition de la hauteur d'eau au seuil de l'instabilité mesurée par une méthode capacitive sera présentée puis par une méthode acoustique dont les principales caractériques seront expliquées.
Surface waves can be generated in the liquid-air interface of a fluid subjected to a vertical vibration (Faraday instability). The waves are stationary (usually half the frequency of the vibration) at the threshold of instability. For a higher amplitude of vibration, they become disordered and provide a canonical example of a dynamic system with plans of spatiotemporal chaos. The internship consists to develop a new measurement method, based on the diffusion of an acoustic wave in the liquid-air interface in order to study these phenomena. At first, the characteristics of the Faraday instability will be discussed in this report then in a second step the transition of the water level at the threshold of the instability measured by a capacitive method will be presented followed by an acoustic method whose the main features will be explained.
1 Instabilité de Faraday - Généralités
Lorsqu’on fait vibrer un fluide verticalement, on observe l’excitation d’ondes de surface pour une accélération supérieure à une valeur critique. Ce phénomène porte le nom d’instabilité de Faraday, et fut découvert en 1831. Les ondes stationnaires excitées s’organisent en formant un motif décrit dans le paragraphe 1.1.
On travaille avec une excitation sinusoïdale de fréquence f contrôlée par un GBF ou par l'amplificateur du vibreur. Il faut régler l'horizontalité du vibreur : il est nécessaire pour avoir une couche d'épaisseur constante et donc des ondes qui se produisent sur toute la surface du fluide en même temps. L’accéléromètre nous permet d’avoir accès à l’accélération réelle de la cuve grâce à un capteur piézoélectrique et d'un amplificateur de charge.
1.1 Caractériques du motif de l'instabilité
L’oscillation de la surface du fluide s’effectue à une fréquence f/2, f étant la fréquence de vibration du piston. L’équation de dispersion des ondes de surface est $$\omega^2=(gk+\frac{\gamma k^3}{\rho}) \tanh(kh)$$ où ω est la pulsation des ondes de surface (ω=πf), ρ est la masse volumique du fluide, γ est la tension superficielle du fluide, ω la pulsation de vibration associée à f, k le nombre d'onde de l'instabilité associé à λ la longueur d'onde du motif et h la hauteur d'eau dans la cuve qui est de telle sorte que tanh(kh)∼1.
1.2 Seuil de l'instabilité de Faraday
L’instabilité de Faraday est observée à partir d’un certain seuil pour l’accélération : il s'agit de l’amplitude la plus faible pour laquelle on observe l’instabilité des ondes stationnaires en partant d’une situation initiale sans instabilité. A cause du phénomène d'hystérésis, les seuils en augmentant l'accélération et en diminuant l'accélération ne sont pas identiques.
Le seuil de l'instabilité augmente avec la fréquence de vibration avec la relation $$\ddot A_c \propto \frac{\rho^{1/3} \nu}{\gamma^{1/3}} (2 \pi f)^{5/3} $$ avec ν la viscosité cinématique du fluide. Cette relation est obtenue par analyse dimensionnelle en supposant l'accélération critique proportionnelle à la viscosité du fluide en négligeant les effets de la gravité, pour cela la fréquence doit être assez élevée pour être en régime capillaire, et la hauteur au repos de la couche de fluide, dans la même limite où la longueur d'onde est petite devant cette hauteur.
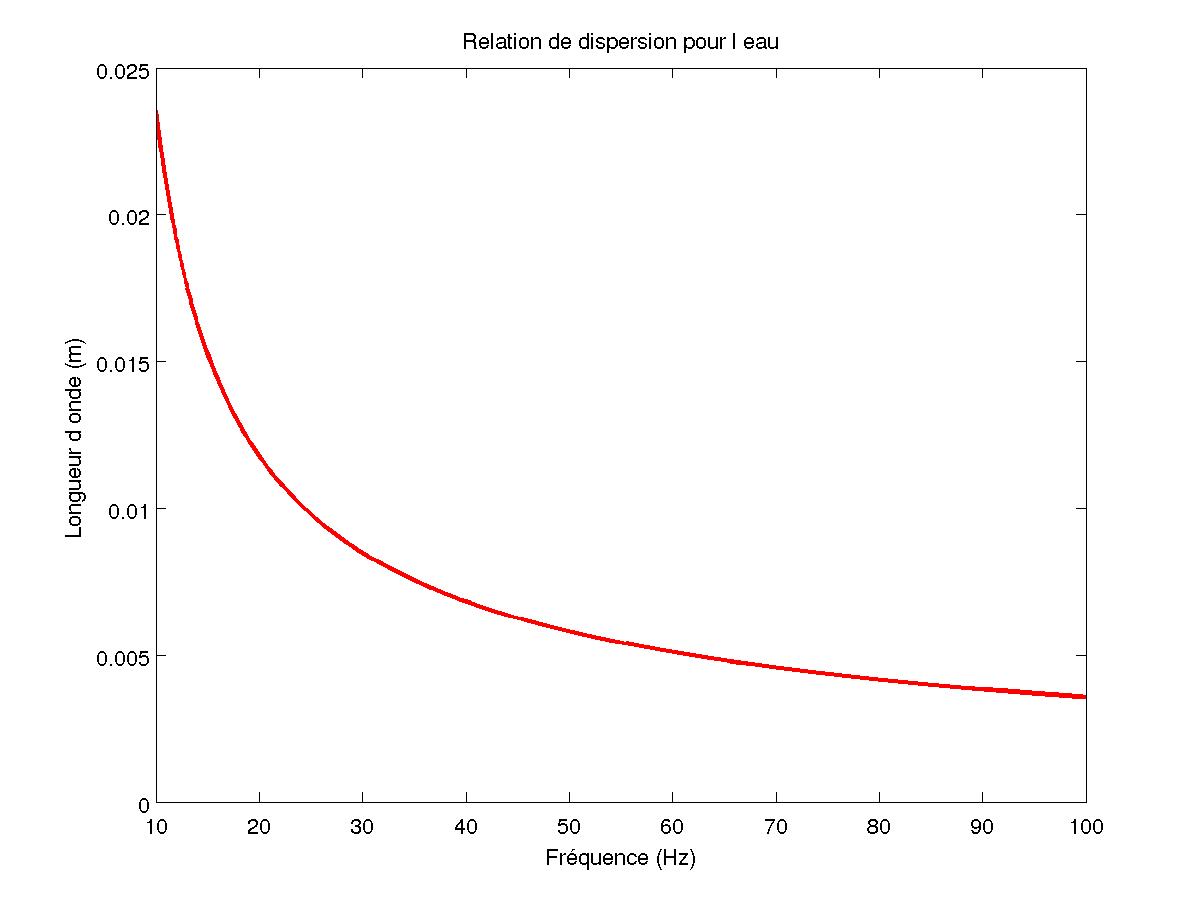
FIG 2 - Relation de dispersion pour l'eau
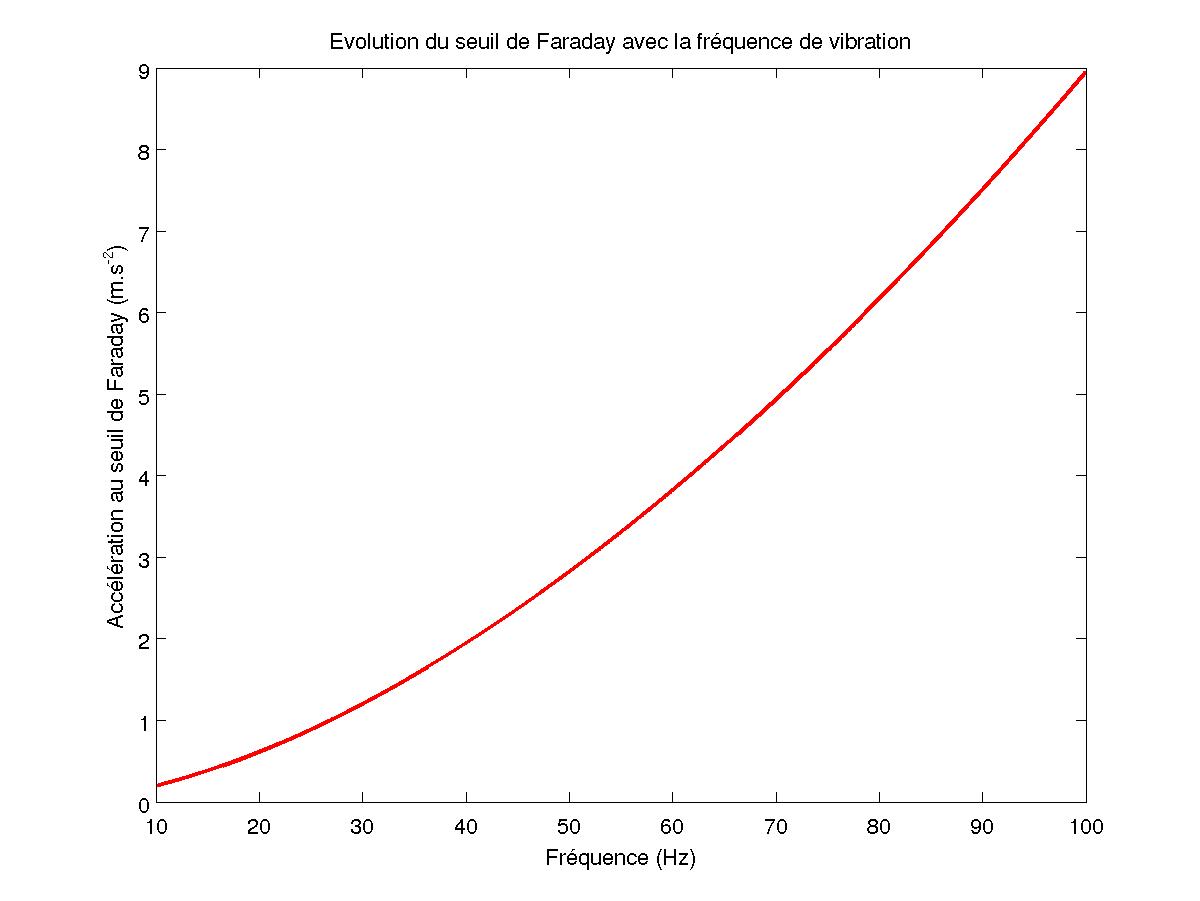
FIG 3 - Evolution du seuil de Faraday
2 Mesure capacitive
2.1 Montage

FIG 4 - Montage du fil capacitif
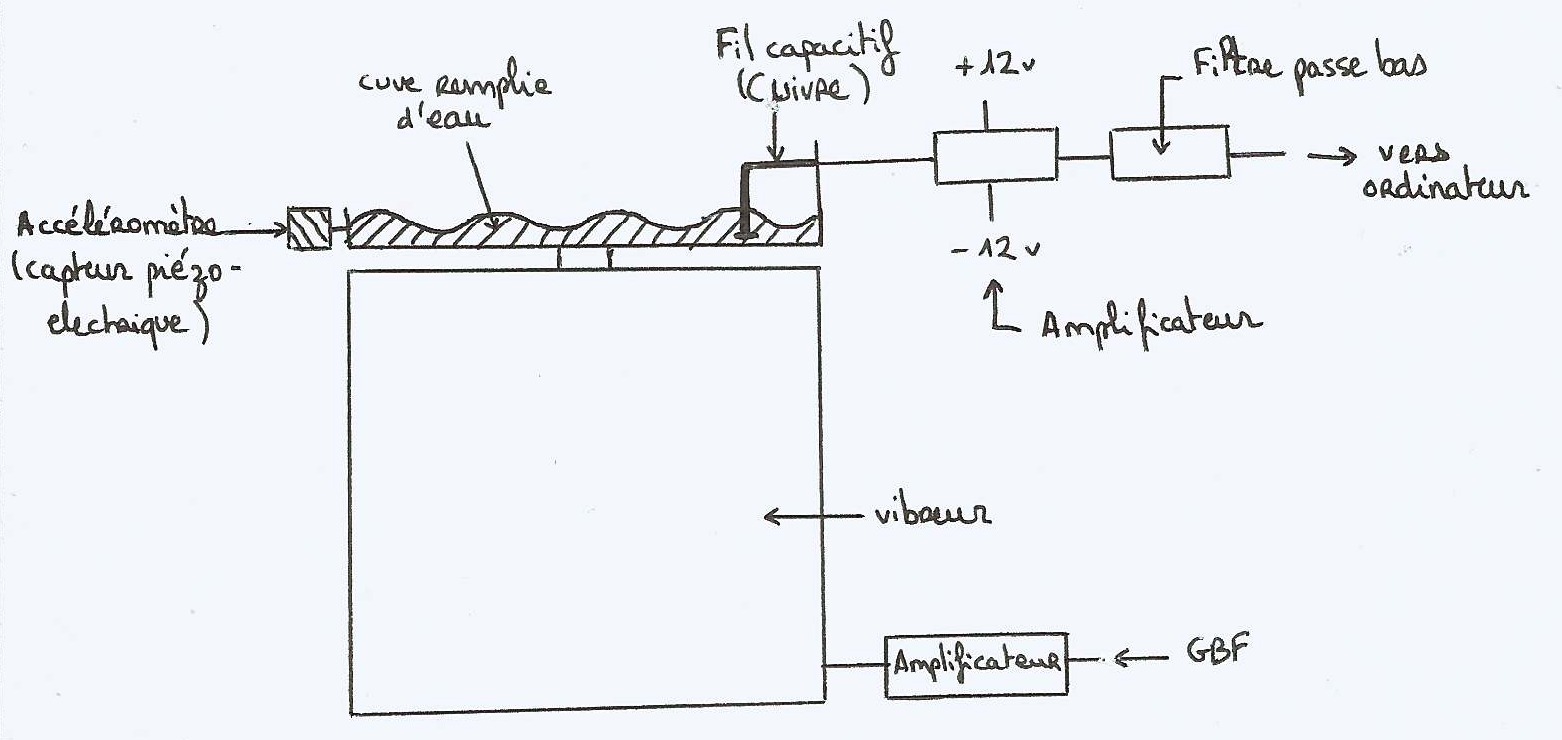
FIG 5 - Schéma du fil capacitif
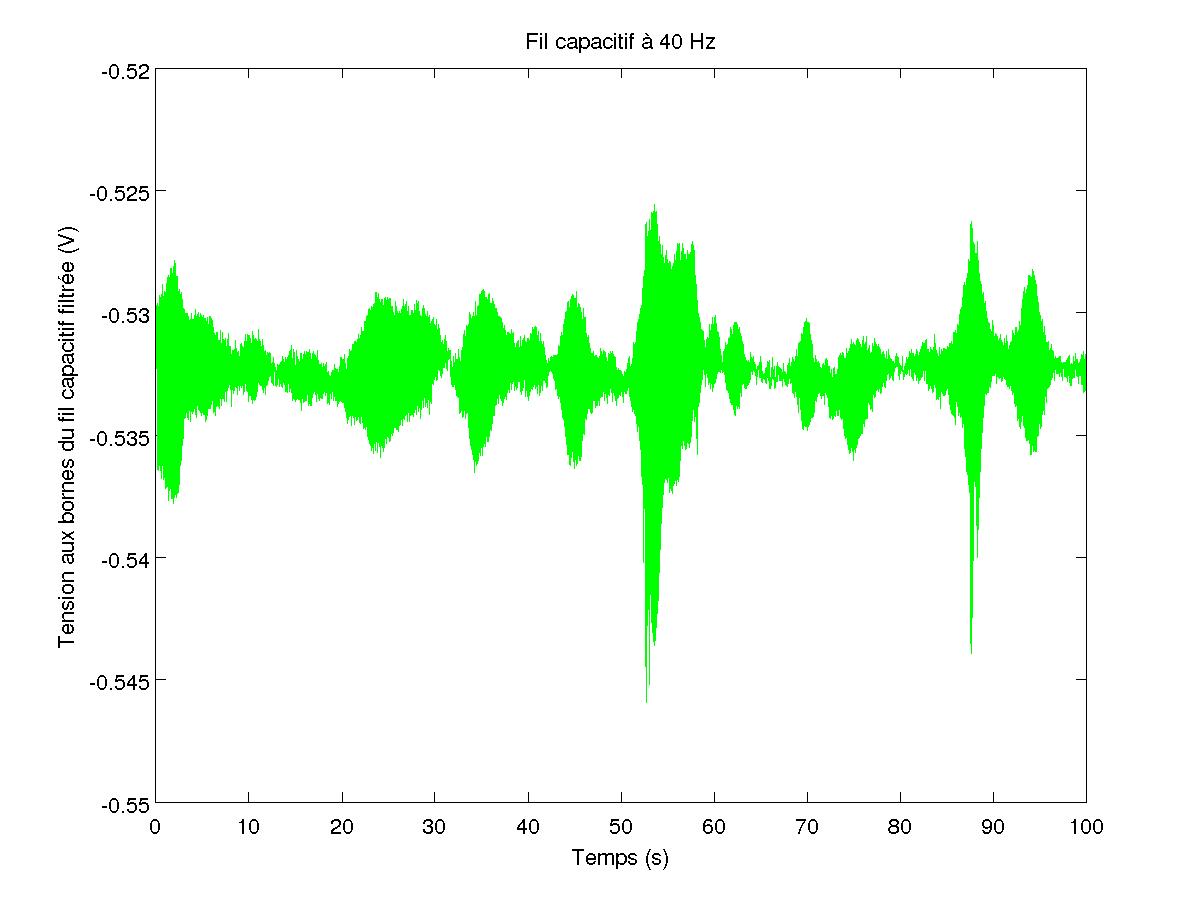
FIG 6 - Tension filtrée aux bornes du fil capacitif

FIG 4 - Montage du fil capacitif

FIG 5 - Schéma du fil capacitif

FIG 6 - Tension filtrée aux bornes du fil capacitif
Ce montage permet de mesurer la hauteur d'eau en utilisant le fait que la capacité d'un fil de cuivre isolé plongé dans l'eau varie. Cette variation est provoquée par la différence entre la constante diélectrique de l'eau 78 par rapport à celle l'air qui est de 1. La hauteur d'eau est proportionnelle à la capacité du fil de cuivre, qui correspond à celle d'un condensateur cylindrique, car cette dernière est proportionnelle à la permittivité diélectrique : $$C=\epsilon_0 \epsilon_r \frac{L}{\ln(b/a)}$$ avec L la longueur du fil dans le milieu, a et b les rayons interne et externe du condensateur. On retrouve la formule du condensateur plan pour des rayons voisins soit b=a+e avec e petit (car e est l'épaisseur du verni isolant autour du fil de cuivre).
On mesure, à l'aide d'une acquisition numérique traitée par le logiciel Labview, l'accélération de la cuve et la tension aux bornes du fil capacitif en fonction du temps en prenant 1000 points par secondes sur une durée de 100 secondes. Les données sont écrites dans un fichier traité par Matlab ultérieurement. Labview permet également de déterminer l'amplitude du signal ainsi que la moyenne et l'écart-type de celui-ci. On filtre la tension aux bornes du fil capacitif pour éliminer les effets d'oscillation du ménisque à la fréquence de vibration f : on simule un filtre passe-bas de coupure 0.75f avec Matlab.
La tension ainsi filtrée varie beaucoup au niveau de l'amplitude moyenne sur quelques périodes (cf figure 6). Cela est dû au fait que le fil capacitif donne une mesure locale de la hauteur d'eau et donc dépend de la position du fil dans l'eau : s'il est dans un noeud, l'amplitude est nulle et s'il est dans un ventre, on obtient la mesure exacte de l'amplitude crète à crète du signal. Le fait de moyenner sur un temps long devant la période de déplacement des noeuds et des ventres des vagues créées par l'instabilité, donne une mesure correcte de l'amplitude des vagues.
2.2 Comportement de l'amplitude des ondes au voisinage du seuil de l'instabilité de Faraday
On obtient les courbes de transition en traçant l'écart-type du signal capacitif filtré en fonction de l'écart-type de l'accélération. L'écart-type donne un meilleur résultat que l'amplitude crète à crète du signal car quelques évènements rares modifient le maximum et le minimum du signal. Pour obtenir la bonne valeur de l'amplitude, il faut multiplier le résultat par √2 car l'écart-type donne la valeur efficace du signal.
On peut trouver le coefficient de proportionnalité entre la hauteur de l'eau et la tension mesurée aux bornes du fil capacitif. Pour cela, on ajoute un volume d'eau connu précisément et on regarde l'augmentation de la tension moyenne du signal. La cuve utilisée a un diamètre de 18.5 cm. En y ajoutant 20 mL d'eau, on trouve que 1 V correspond à 2.8 mm d'eau.
On obtient des droites lorsque l'on trace l'amplitude des vagues au carré en fonction de l'accélération.
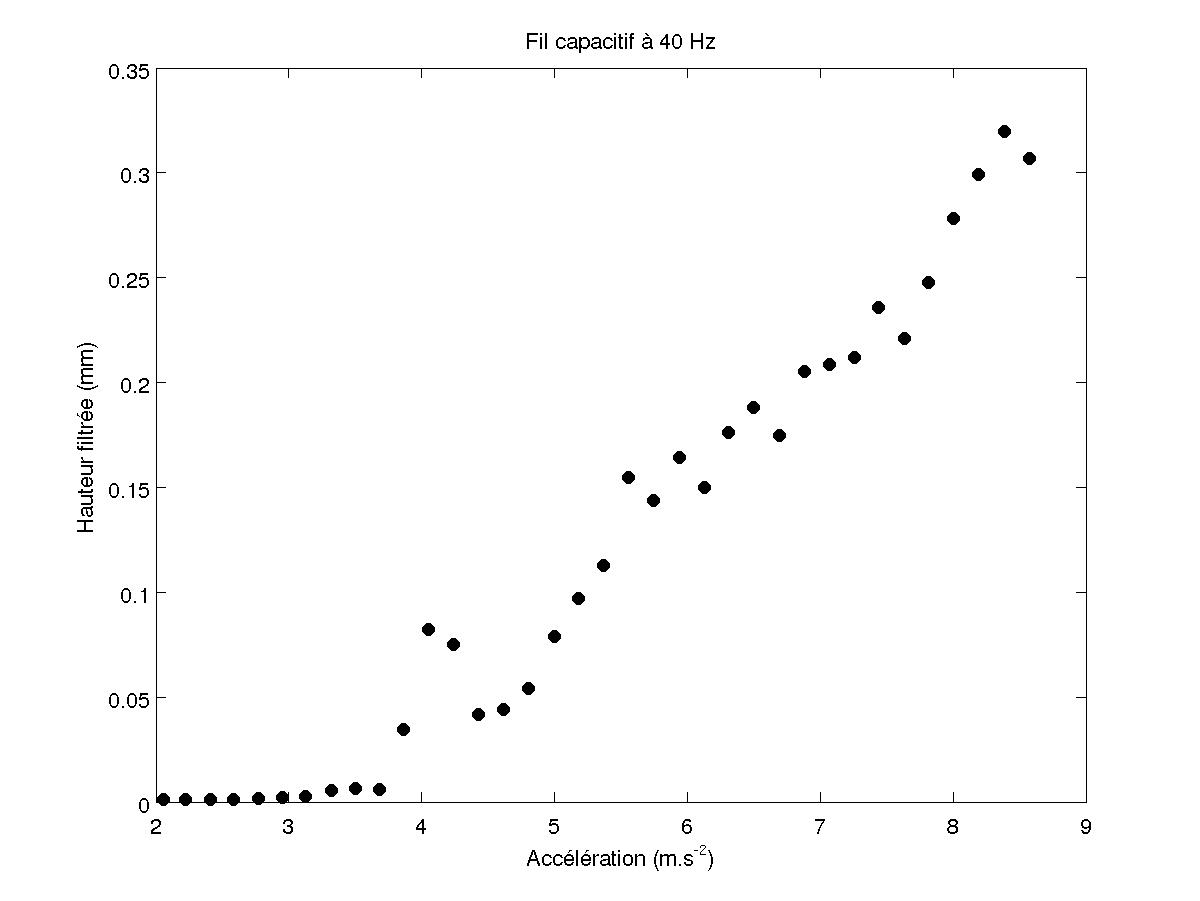
FIG 7 - Transition pour 40 Hz
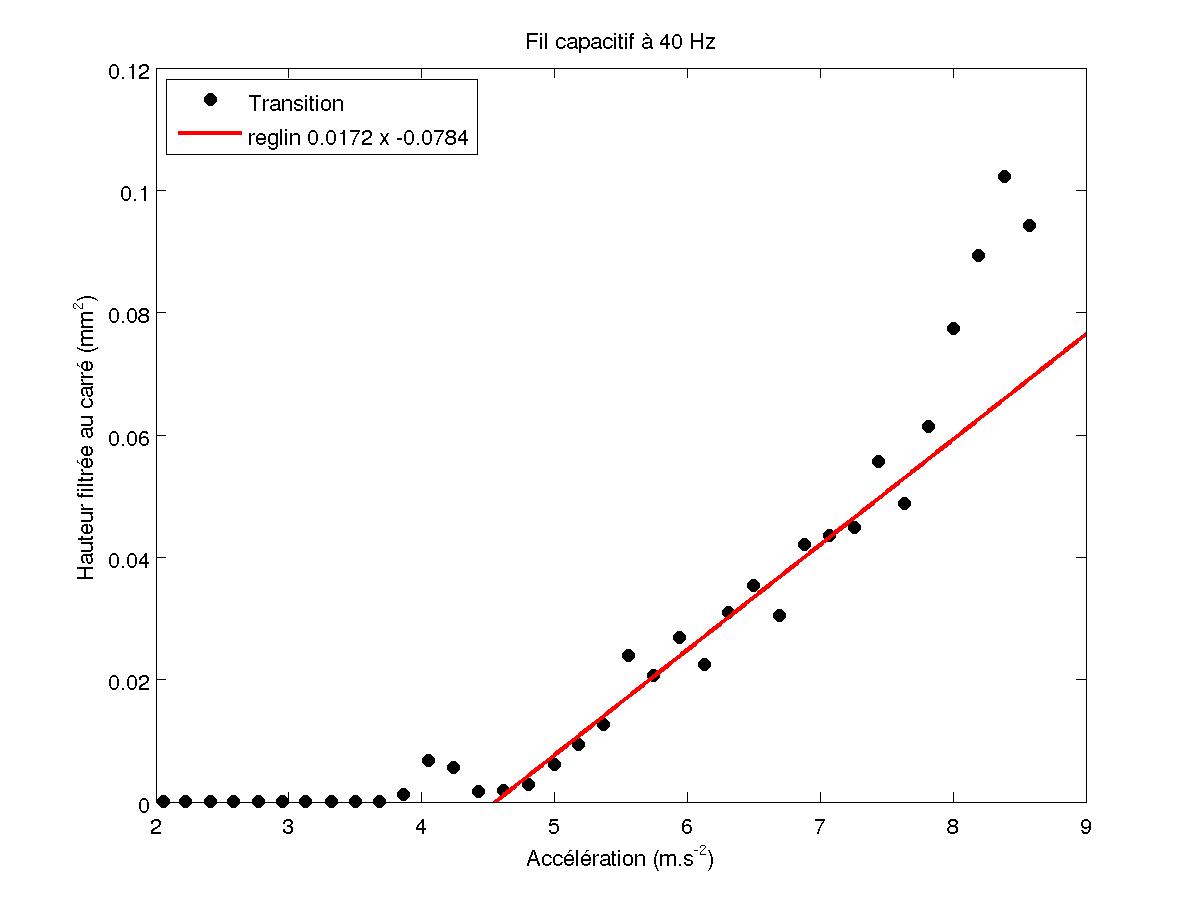
FIG 8 - Transition pour 40 Hz
2.3 Evolution du seuil de l'instabilité de Faraday avec la fréquence de vibration
On regarde d'abord l'évolution du seuil en fonction de la fréquence de vibration en reportant l'abscisse à l'origine de toutes les droites obtenues précédemments. On trouve une courbe proche de la théorie. Puis on trace l'évolution de la pente au seuil, en reportant la pente des précédentes droites.
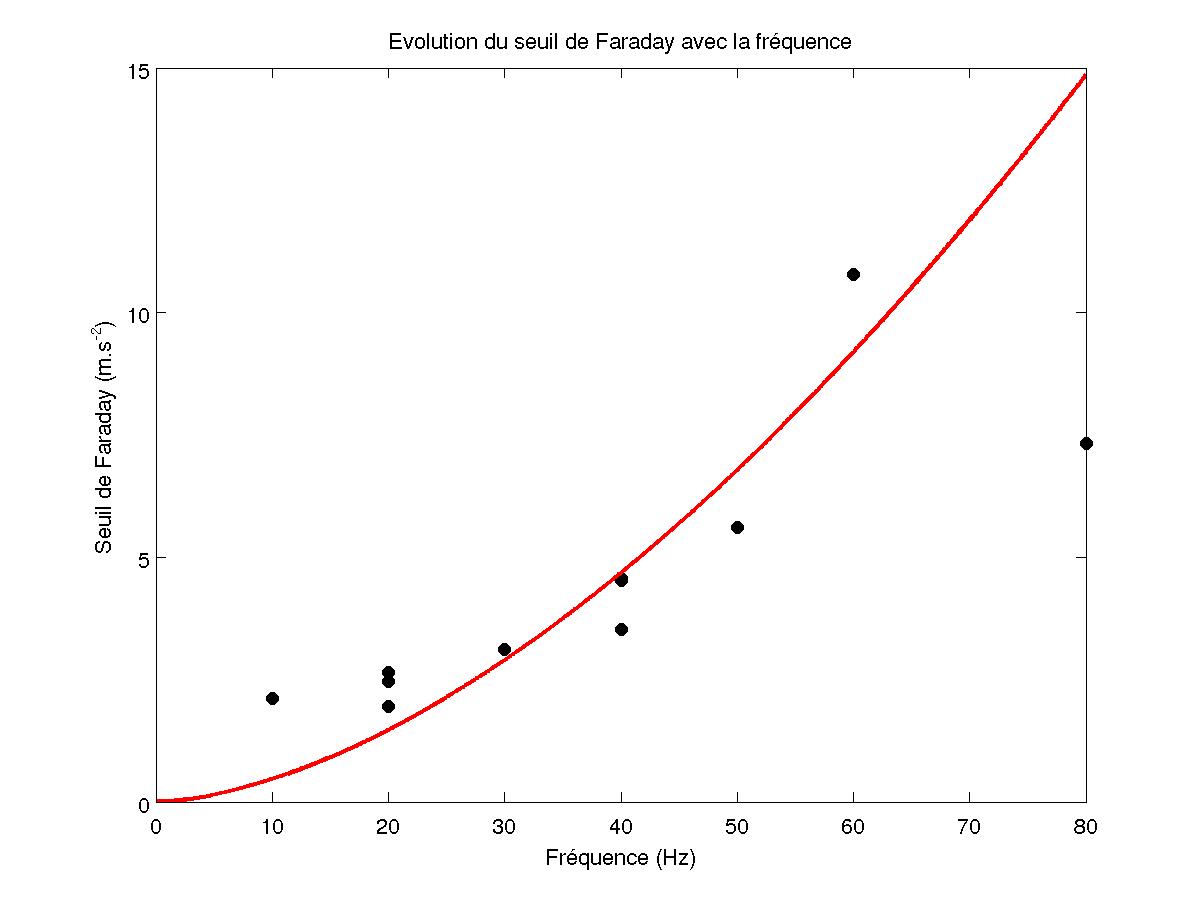
FIG 9 - Evolution du seuil
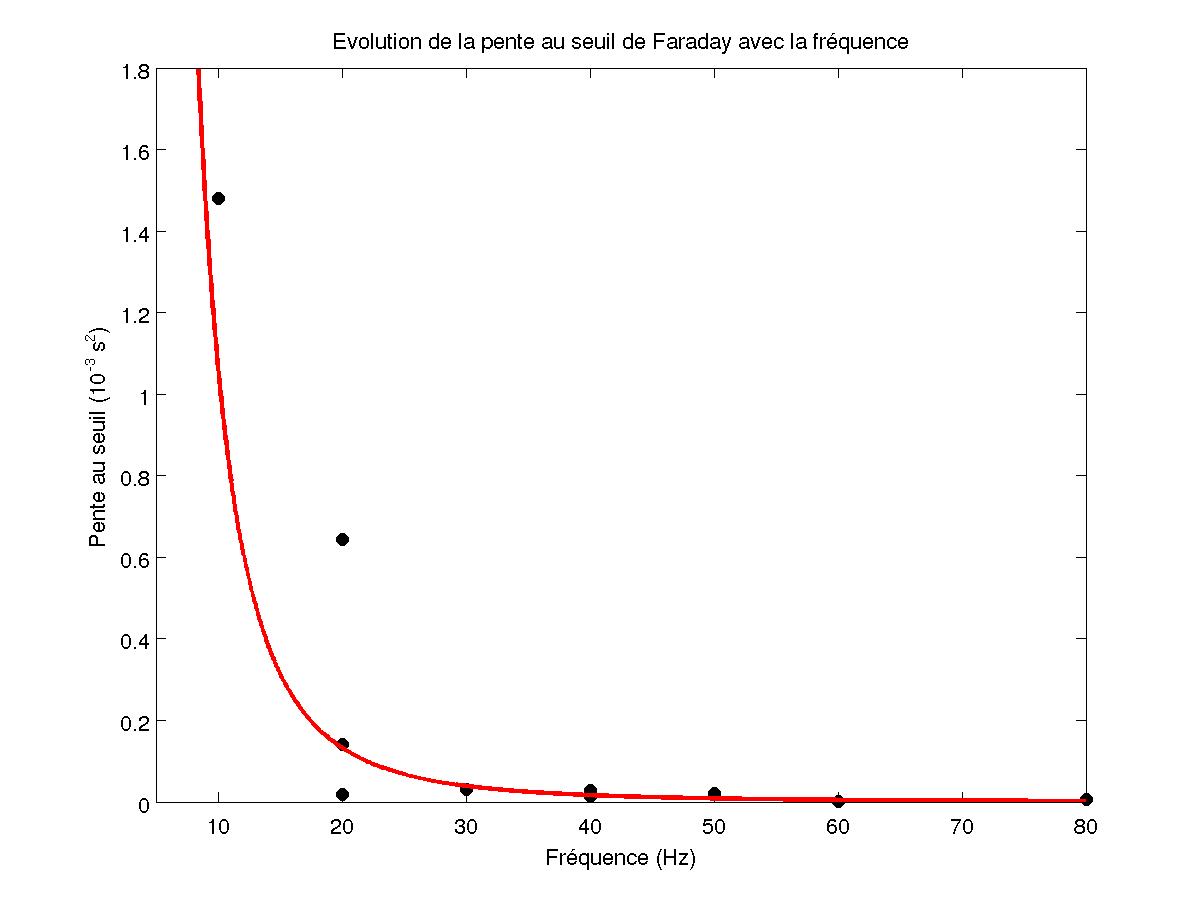
FIG 10 - Evolution de la pente au seuil
On s'aperçoit alors que le seuil augmente avec la fréquence comme prévu par l'analyse dimensionnelle de la section 1.2 et que la pente au seuil diminue comme f -3 (obtenue avec une corrélation de 0.85).
3 Mesure acoustique
3.1 Montage
On envoie une onde sonore sinusoïdale de fréquence F, correspondant à la fréquence de résonance des transducteurs acoustiques, et d'amplitude A∼10 V. On fait vibrer sinusoïdalement la cuve à la fréquence f, avec une accélération mesurée par l'accéléromètre. On change la tension délivrée par le GBF alimentant le vibreur ou le gain de l'amplificateur, de valeur inconnue.
Pour les premières mesures, on utilise une incidence normale, α=0 avec des transducteurs à 150 kHz. Puis dans un second temps, on utilisera des transducteurs à 90 kHz. On prendra alors un angle α d'incidence de π/4.
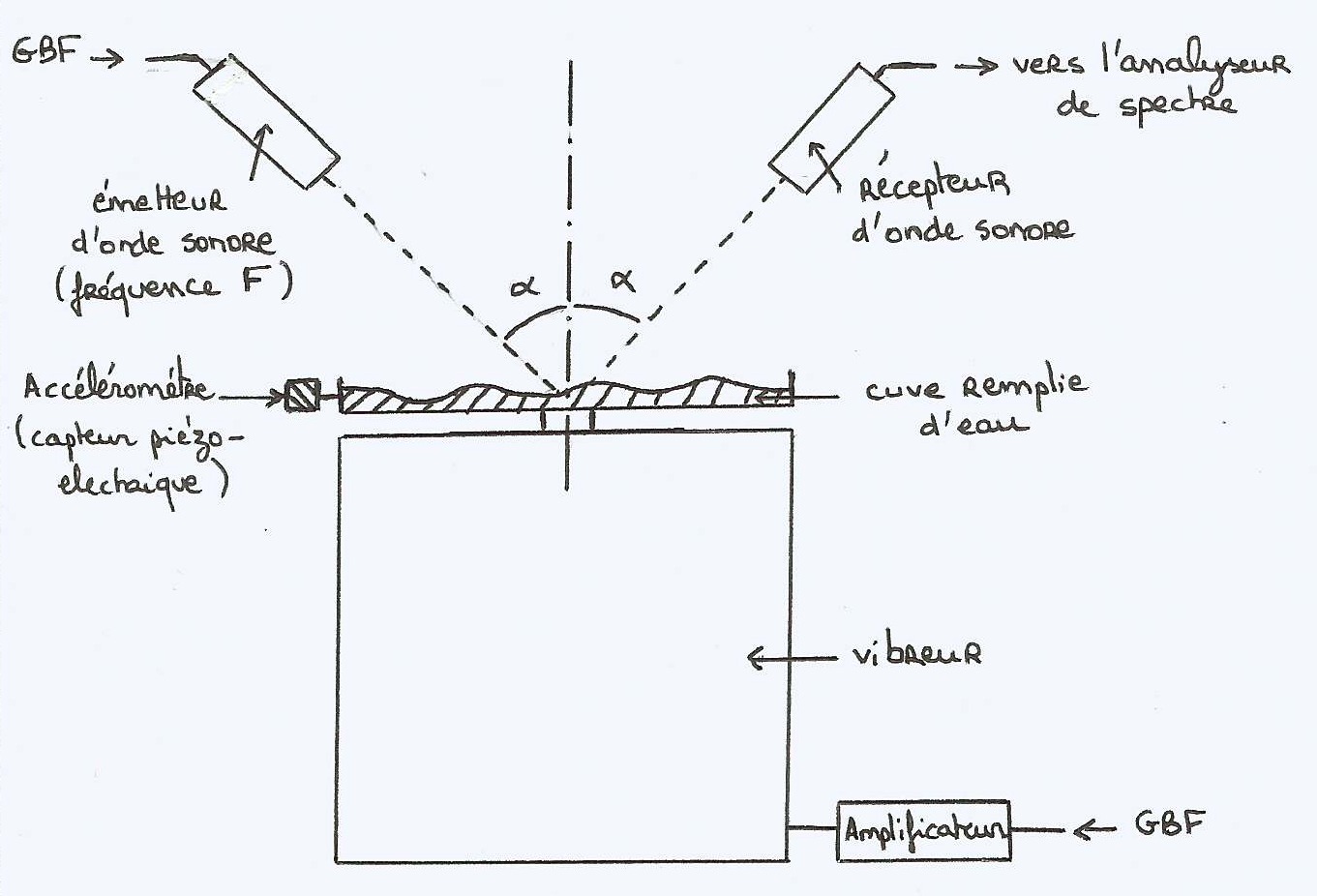
FIG 11 - Schéma du montage

FIG 12 - Photo du montage
Pour pouvoir obtenir les courbes qui suivent, on effectue les règlages de l'analyseur de spectre pour obtenir une mesure rapide, tout en ayant une bonne précision en moyennant sur plusieurs secondes.
La fréquence de résonance du transducteur dépend de la raideur (module d'Young) et de la densité du matériau utilisé pour fabriquer le transducteur et de ses dimensions. Il faut se mettre à résonance car c'est là qu'il y aura l'amplitude de vibration maximale du transducteur pour un forcage donné. On trouve alors les valeurs de 146.3 kHz et 90.3 kHz pour les deux types de transducteurs utilisés.
3.2 Caractéristique d'une onde sonore réfléchie par une surface vibrante
On fait varier l'amplitude des vibrations du piston, pour cela il vaut mieux augmenter la tension du GBF directement au lieu d'augmenter le rapport d'amplification dont on ne peut pas connaître la valeur. On obtient la courbe suivante à l'aide de l'analyseur de spectre :
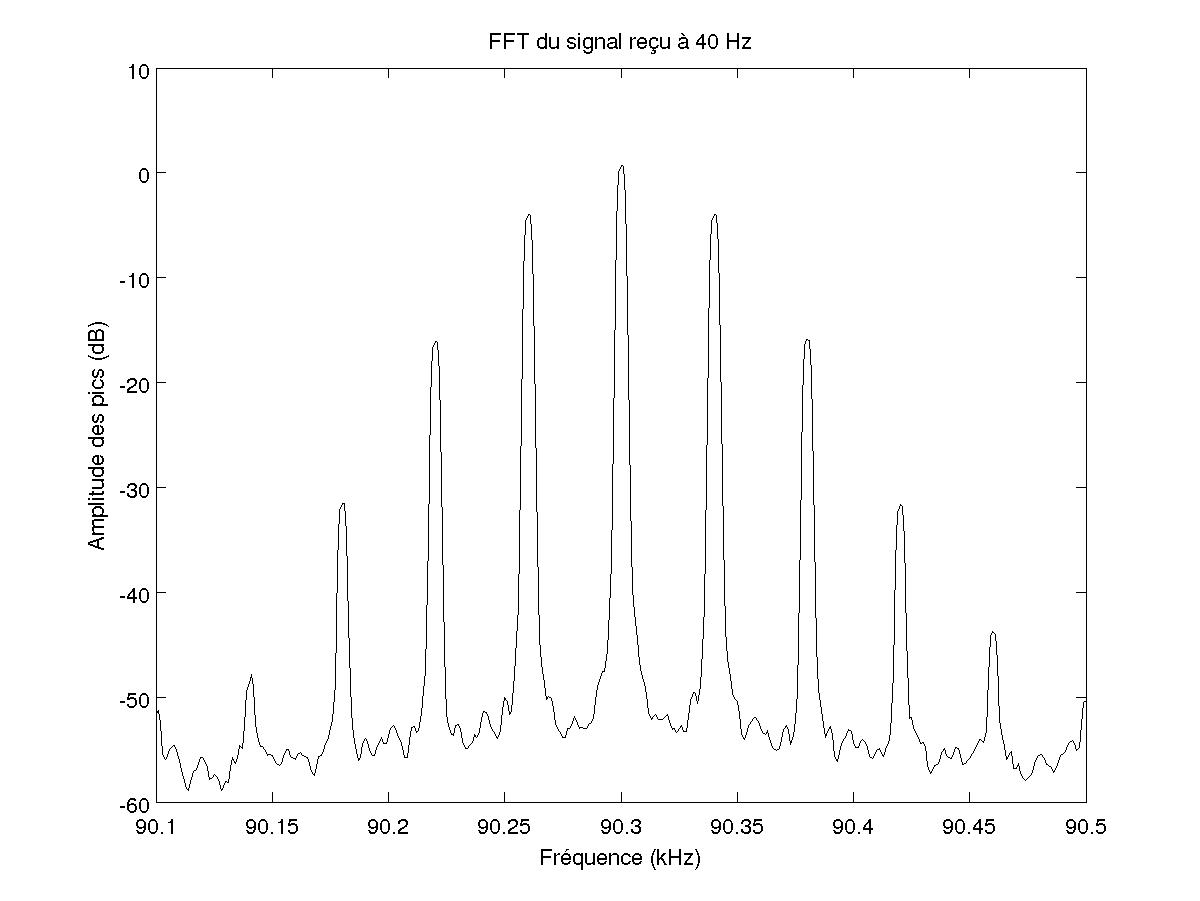
FIG 13 - FFT du signal pour 40 Hz
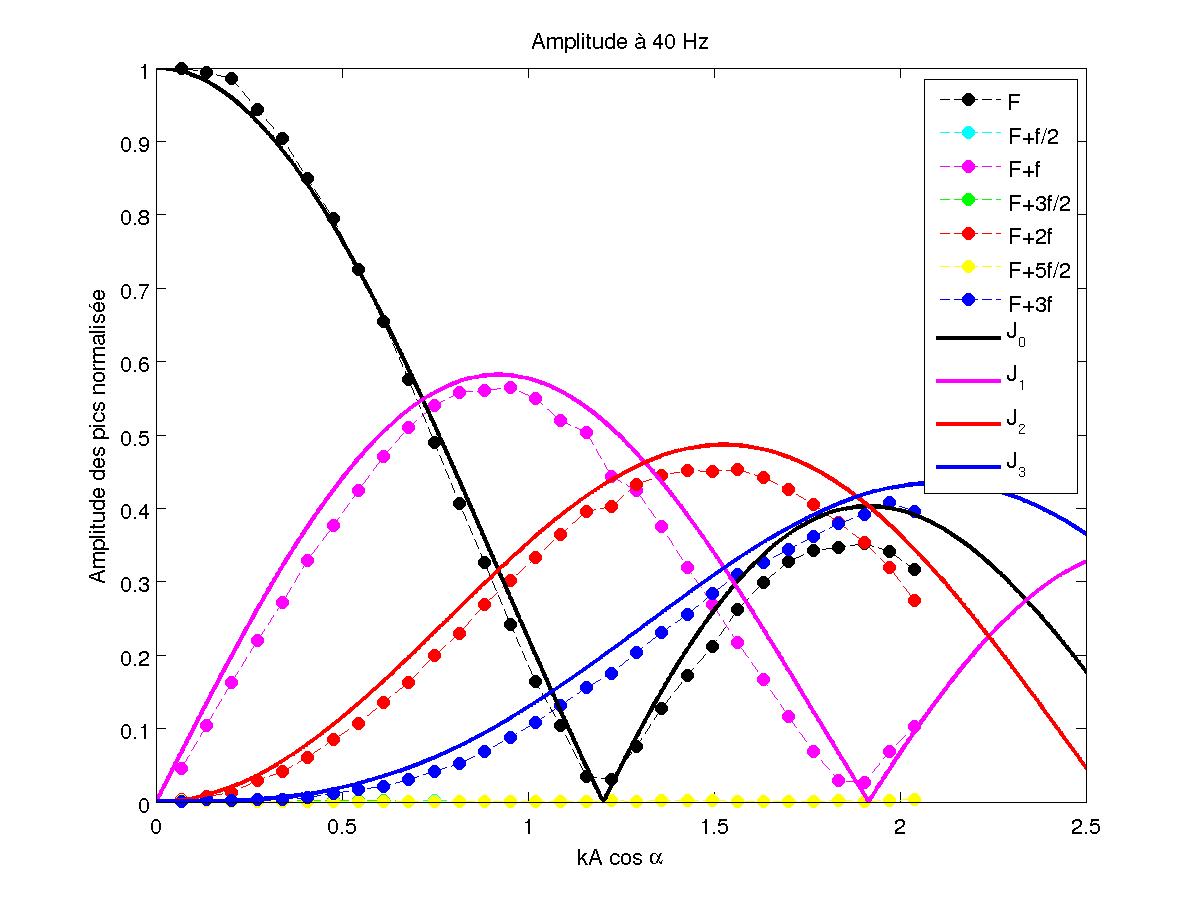
FIG 14 - Amplitude des pics en fonction de kA pour 40 Hz
Lorsque l'accélération du piston augmente, l'amplitude des pics varient. Les fréquences de ces pics sont F±n.f avec n entier et aucun pour une fréquence moitié au contraire du cas avec l'instabilité de Faraday (cf paragraphe 3.4). On trouve alors la courbe de l'amplitude des pics en fonction de l'accélération de la figure 14.
On renormalise les courbes de la manière suivante : $kA=\frac{2 \pi F}{c} \frac{A_{cc}}{(2 \pi \Omega)^2}$ en abscisse. Et en ordonnée, on veut l'amplitude des pics : $A_p=10^\frac{A_{p_{dB}}}{20}$, avec $A_{p_{dB}}$ l'amplitude en décibel obtenue par l'analyseur de spectre. Puis on renormalise les amplitudes en prenant pour référence l'amplitude du pic central quand le piston est immobile.
3.2.1 Calculs théoriques d'après [1] et [2]
La surface vibre à la fréquence f, on a donc l'équation de la surface suivante : ζ(t)=A sin(2πft). L'onde acoustique envoyée avec une incidence normale sur le piston a pour pulsation ω=2πF et nombre d'onde $k=\frac{2\pi}{\lambda}$, λ correspondant à la longueur d'onde. Elle se propage à la vitesse c=ω/k. Le temps d'aller retour est donc $\tau(t)=\frac{2}{c}[L-\zeta(t-\frac{\tau(t)}{2})]$ avec L la distance entre le piston et les transducteurs. Si A≪L, ce qui semble correct du point de vue expérimental, on a $\tau(t) \sim \frac{2 L}{c}$ et si $\frac{Af}{c} \ll 1$ on peut remplacer ce résultat dans l'expression de ζ(t). L'onde reçue a pour forme : $$\exp(i\omega(t-\tau(t)) \sim \exp(i\omega[t+\frac{2}{c}\zeta(t-\frac{L}{c})])=\exp(i[\omega t+ 2 k A\sin(2\pi f(t-\frac{L}{c}))])$$ Or $$\exp(2ikA\sin(2\pi f(t-\frac{L}{c})))=\sum_{n=-\infty}^{\infty} J_n(2kA) \exp(2 i n\pi f(t-\frac{L}{c}))$$ Donc les fréquences reçues sont F±n.f et ont pour amplitude Jn(2kA), fonctions de Bessel d'ordre n définies comme : $$J_n(x)=\frac{1}{\pi} \int_{0}^{\pi} \cos(nt-x \sin(t)) dt = \sum_{p=0}^{\infty}\frac{(-1)^p}{p!(n+p)!}(\frac{x}{2})^{2p+n}$$
Dans le cas d'une incidence non normale, avec un angle α, correspondant à la figure 11, les résultats sont modifiés par : 2kA → (kz+knz) avec kz= k cos α et $k_{nz}=\sqrt{(\frac{\omega+2\pi nf}{c})^2-k^2 \sin^2 \alpha}$. Si f ≪F alors kz+knz=2kA cos α. D'où, l'amplitude des pics aux fréquences F±n.f évoluent comme Jn(2kA cos α).
3.2.2 Amplitudes expérimentales
On réalise une mesure pour F=90.3 kHz et α=π/4 avec une vibration du piston à 20 Hz. On trouve un résultat très proche de la théorie :l'amplitude des pics varient selon les fonctions de Bessel d'argument 2kA. On observe également, grâce aux figures 17-18-19-20, que ces courbes ne dépendent pas de la fréquence de vibration f du piston.
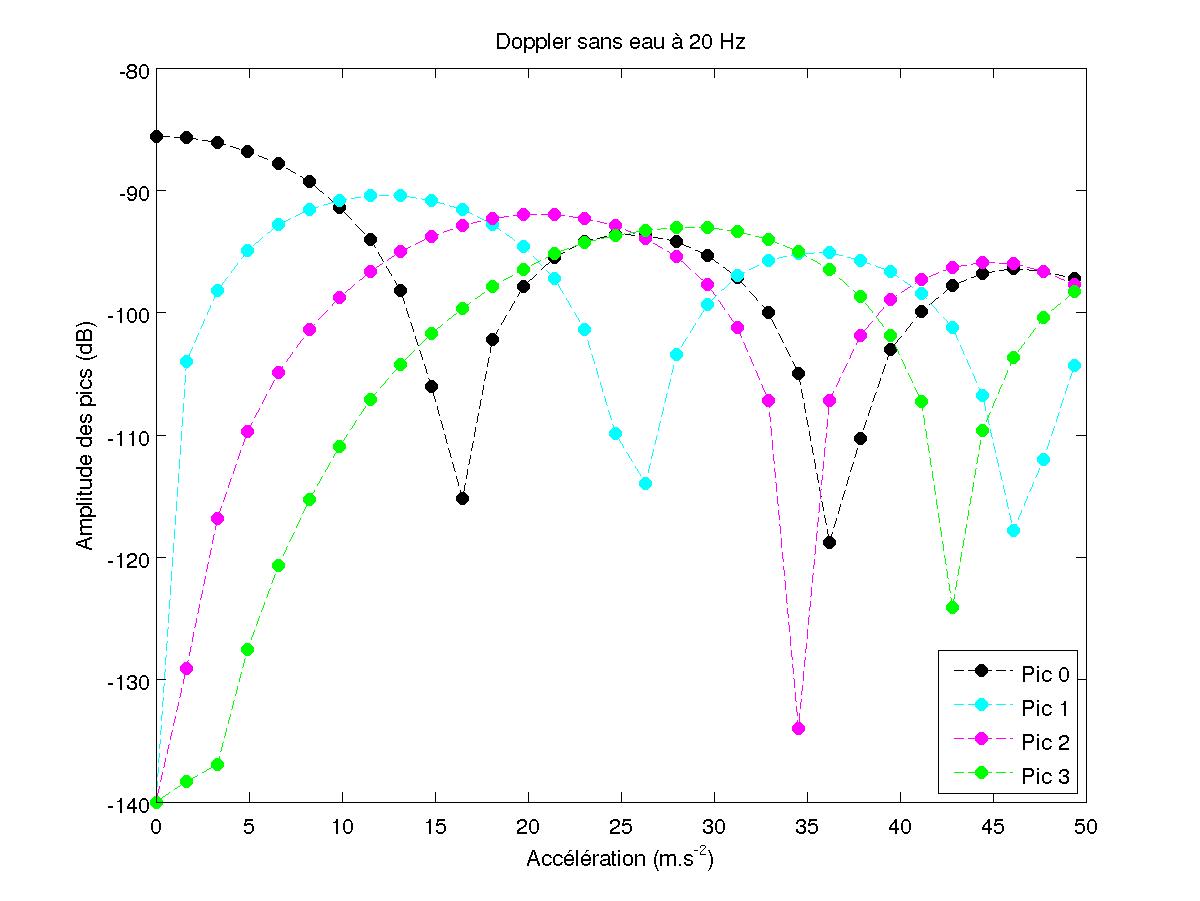
FIG 15 - Amplitude pour 20 Hz en décibels
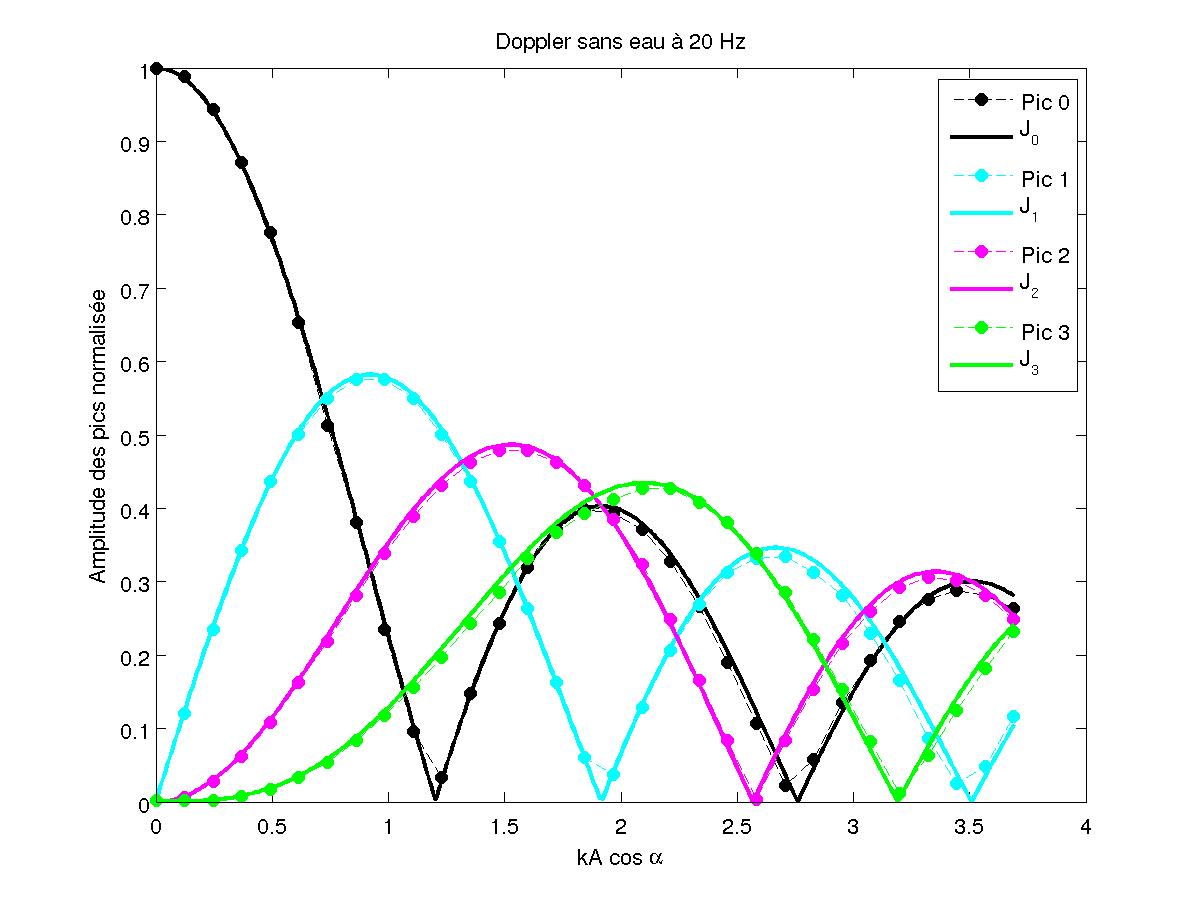
FIG 16 - Amplitude normalisée pour 20 Hz
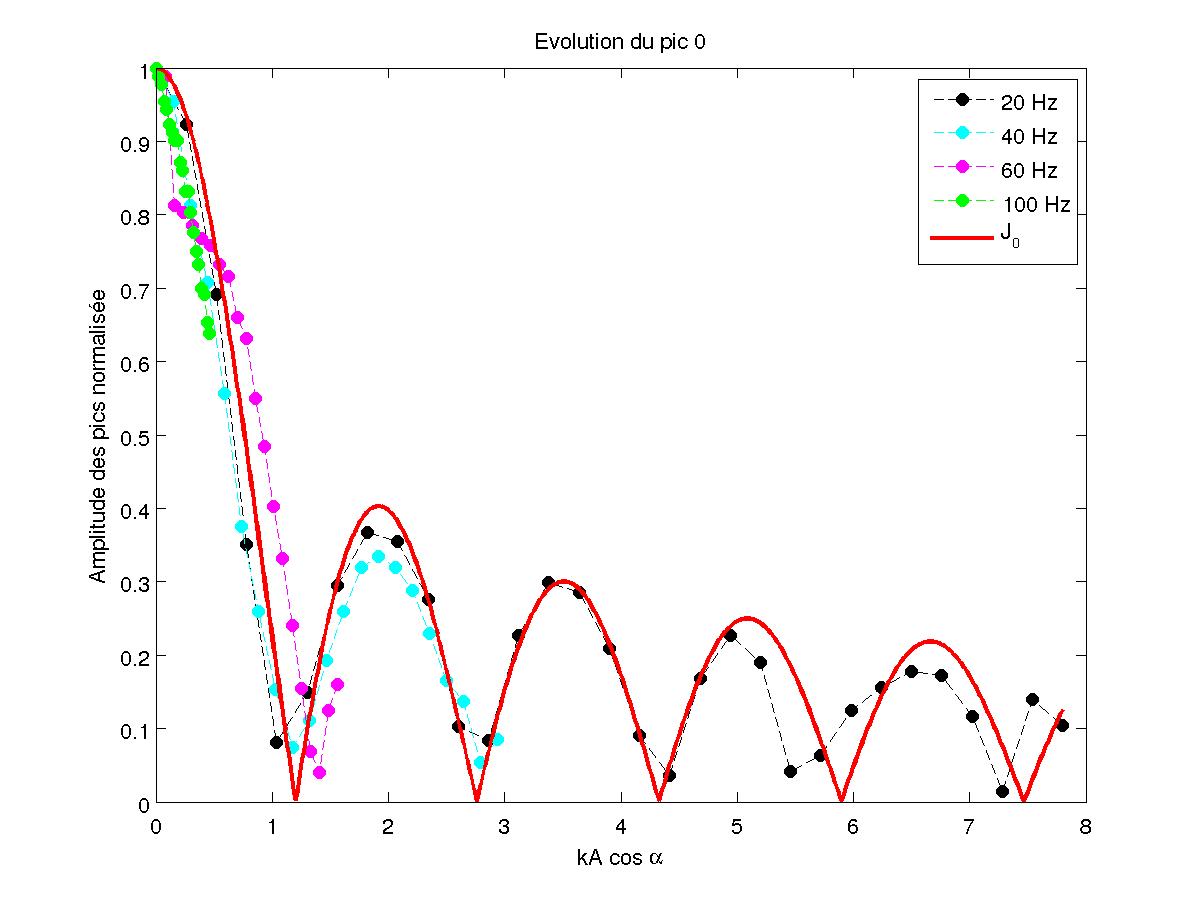
FIG 17 - Amplitude du pic 0 en fonction de kA pour différentes fréquences
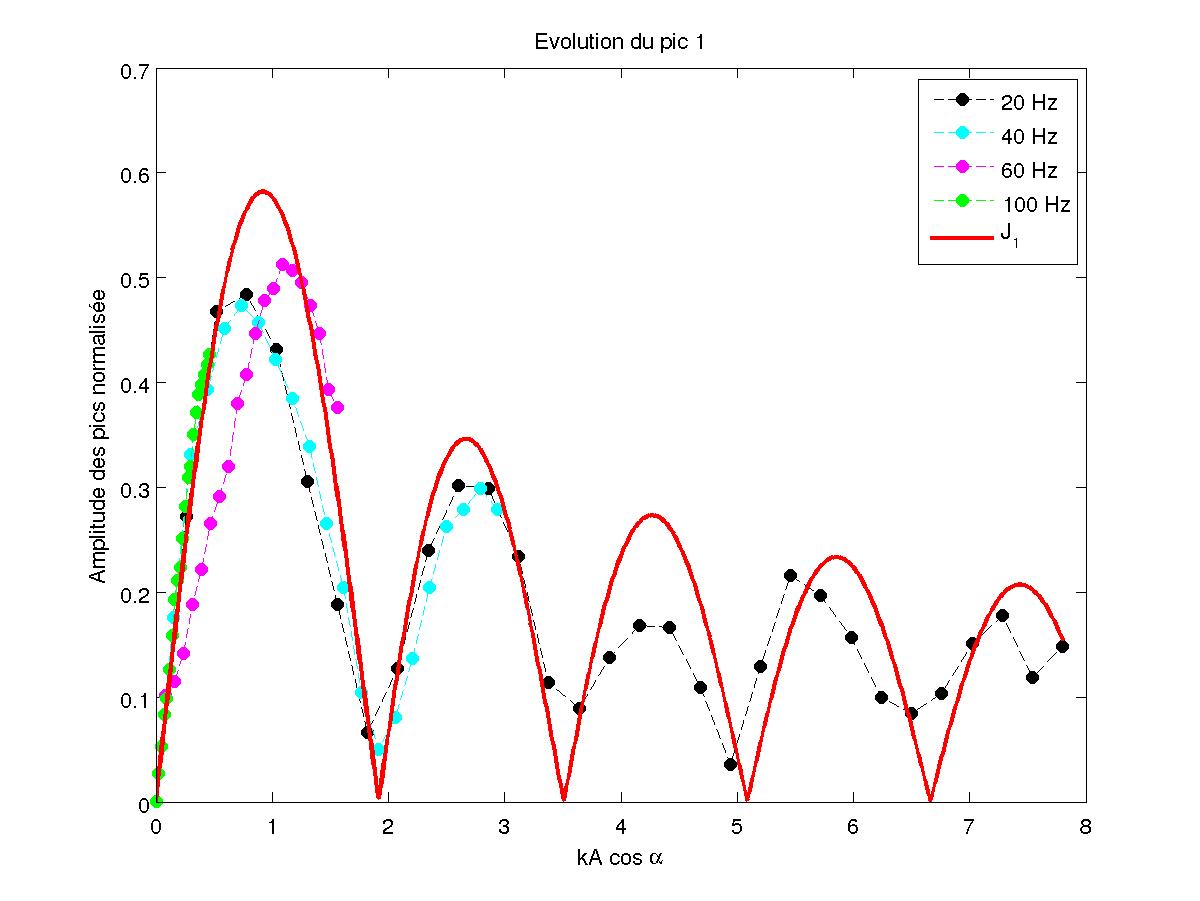
FIG 18 - Amplitude du pic 1 en fonction de kA pour différentes fréquences
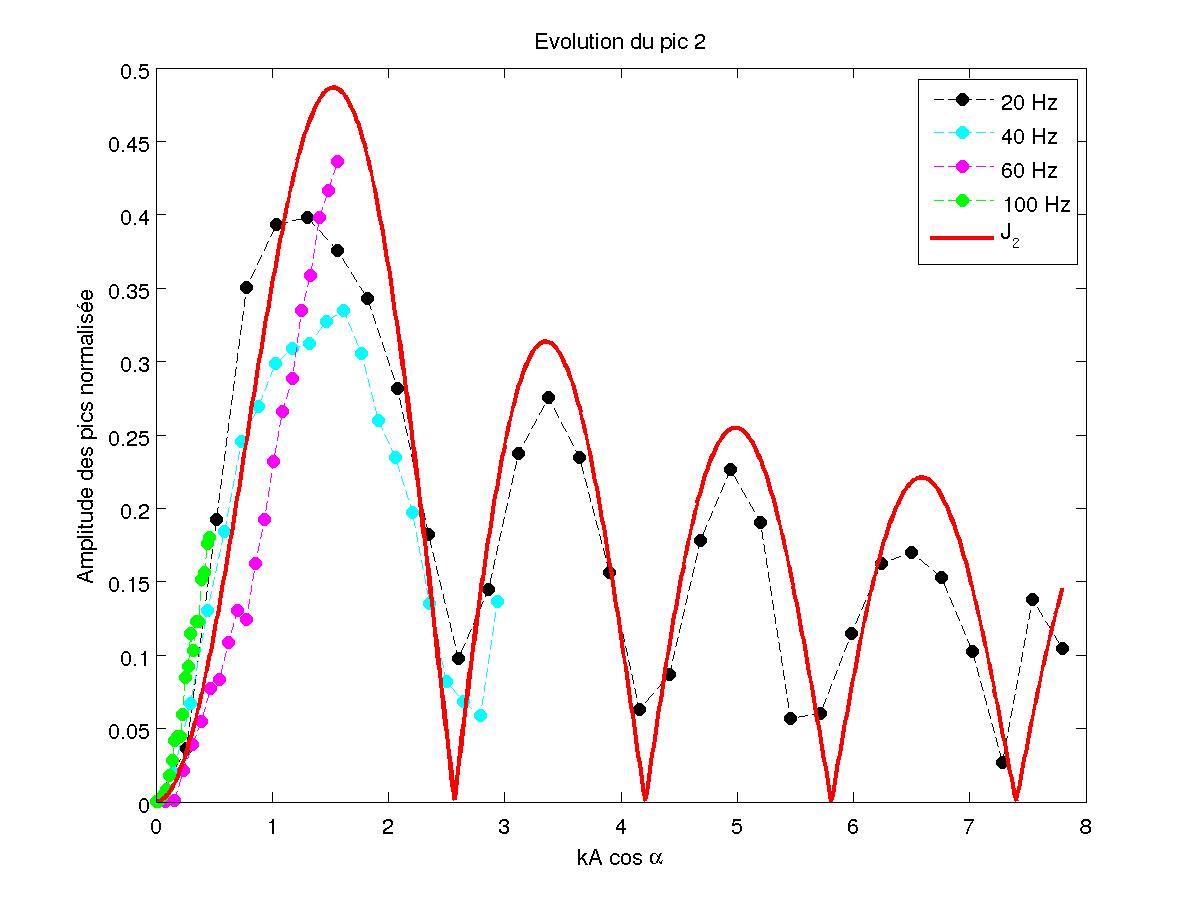
FIG 19 - Amplitude du pic 2 en fonction de kA pour différentes fréquences
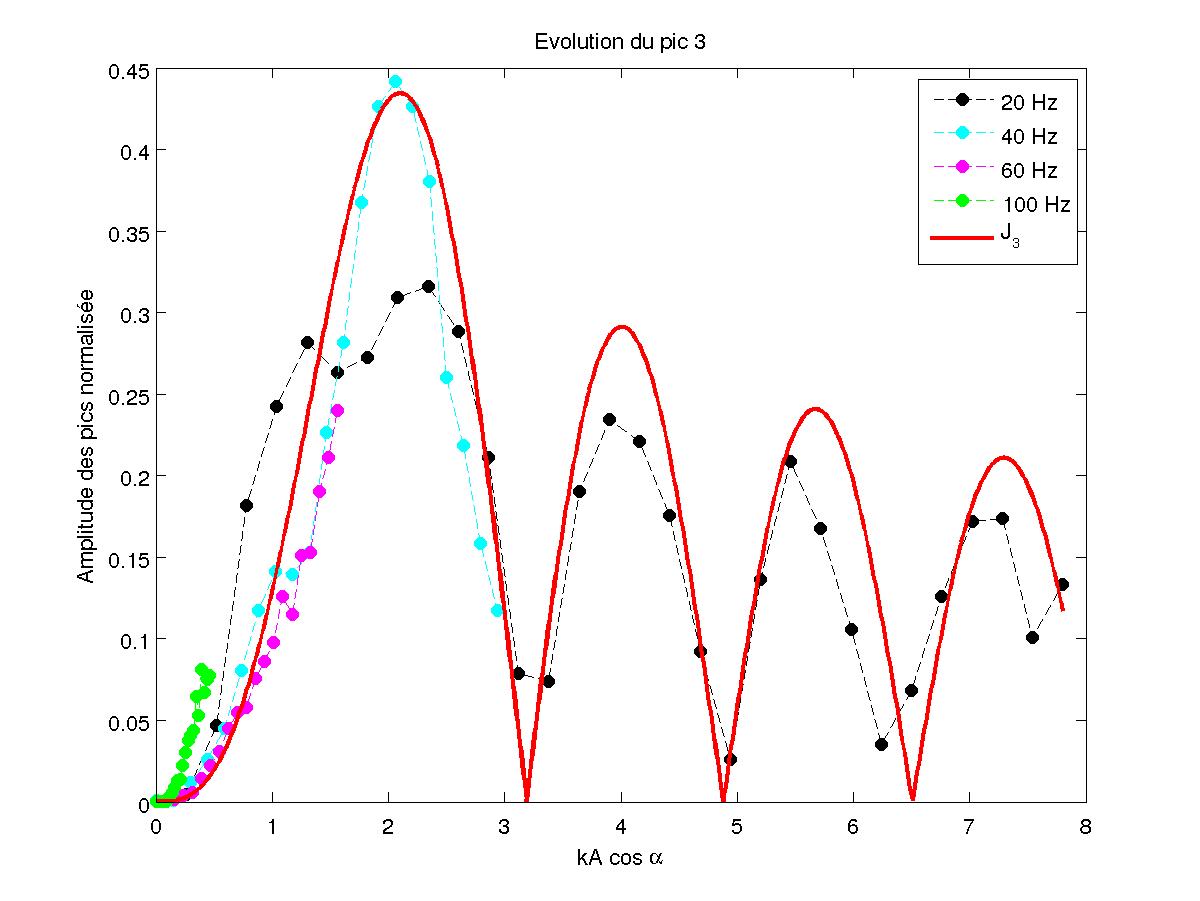
FIG 20 - Amplitude du pic 3 en fonction de kA pour différentes fréquences
3.3 Caractéristique d'une onde sonore réfléchie par une surface ondulée
On vient de voir les caractériques pour une surface plane. Or, lors de l'instabilité de Faraday, la surface est sinusoïdale. On cherche à voir les différences avec les précédents résultats pour une surface ondulée.
3.3.1 Surface ondulée immobile d'après [3]
Pour une surface ondulée d'équation ζ(x)=h cos(px) avec p=2π/λs, λs correspondant à la longueur d'onde de la surface. L'onde acoustique envoyée avec une incidence α a pour pulsation ω=2πF et nombre d'onde k=2π/λ, λ correspondant à la longueur d'onde. Elle se propage à la vitesse c=ω/k. L'amplitude de l'onde diffusée d'ordre n est Jn(2kh cos α).
3.3.2 Surface ondulée vibrant à la fréquence f
On réalise d'abord un montage avec des pailles de diamètre 0.52 mm, longueur d'onde obtenue par instabilité de Faraday pour une vibration à 58.5 Hz de la couche d'eau d'après la section 1.1. Puis on réalise un montage avec des tubes en aluminium de 124 mm de long et de 10 mm de diamètre, cela correspond à une vibration de 20 Hz des vagues, situation plus proche des mesures de l'instabilité de Faraday du paragraphe 3.4. En superposant les courbes, on obtient presque des fonctions de Bessel, ne dépendant pas trop de la fréquence de vibration.

FIG 21 - Montage de la plaque ondulée (pailles)

FIG 22 - Montage de la plaque ondulée (tubes d'aluminium)
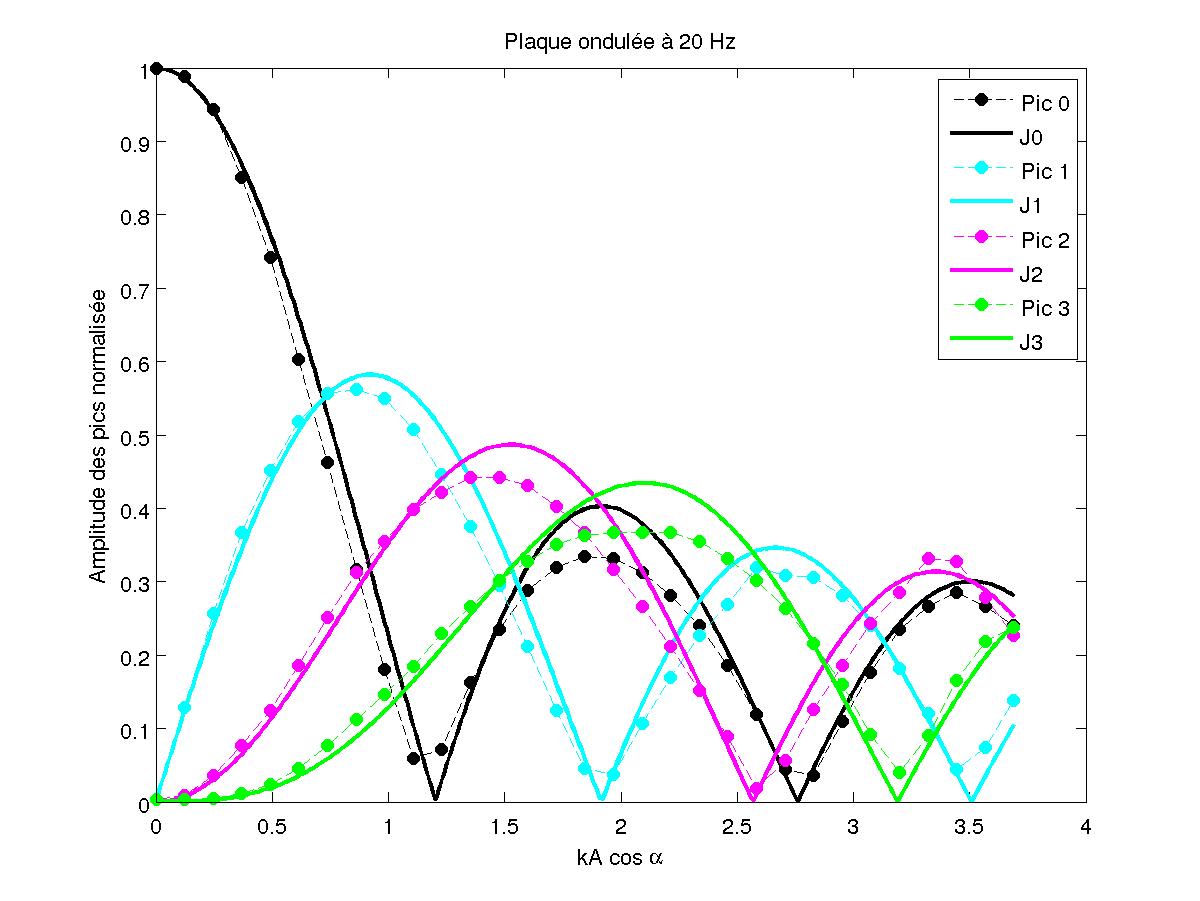
FIG 23 - Mesure à 20 Hz pour les pailles
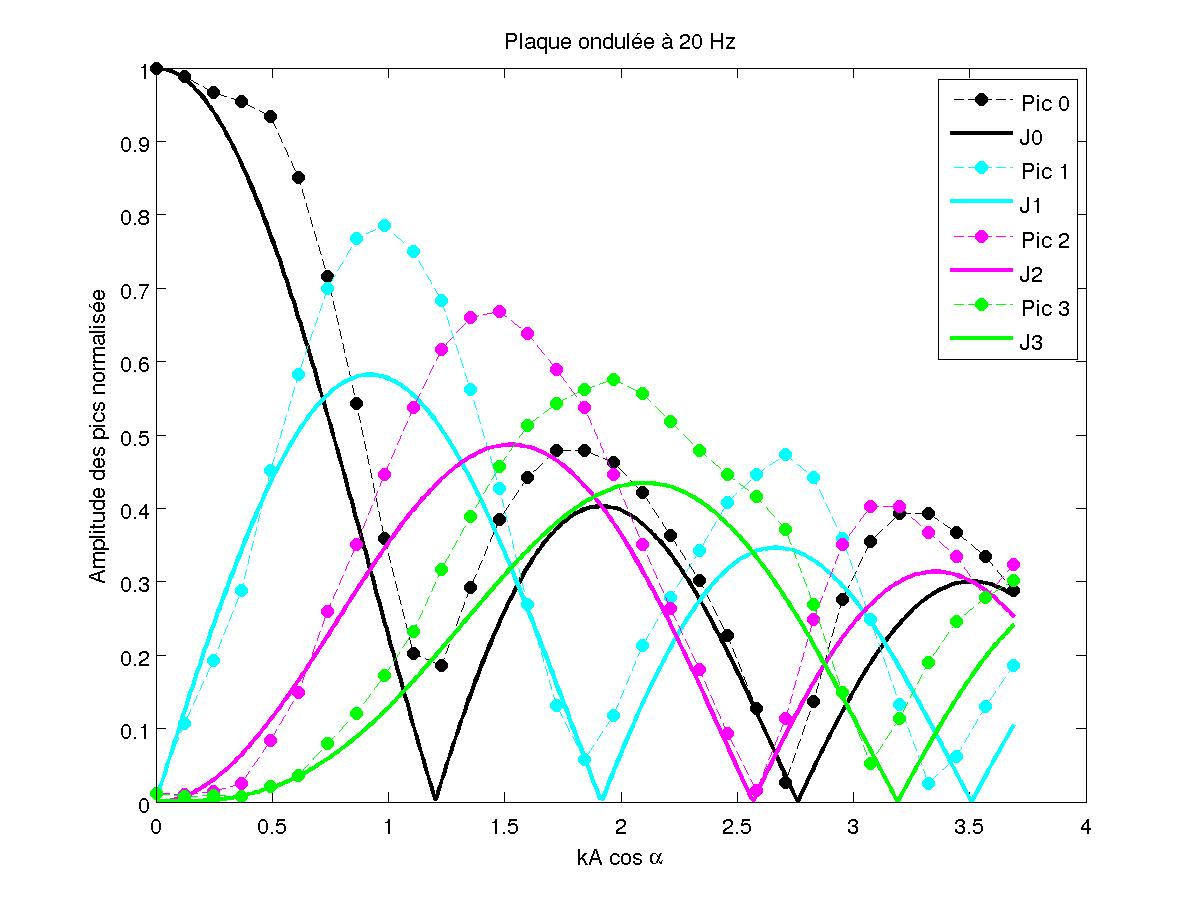
FIG 24 - Mesure à 20 Hz pour les tubes d'aluminium
On peut considérer que l'on a des fonctions de Bessel sur la partie intéressante pour l'instabilité de Faraday (première et deuxième monotonies des fonctions de Bessel).
3.4 Résultats pour une surface liquide (eau) - Instabilité de Faraday
On obtient la courbe suivante à l'aide de l'analyseur de spectre et la courbe de l'amplitude des pics en foncion de l'accélération correspondante.
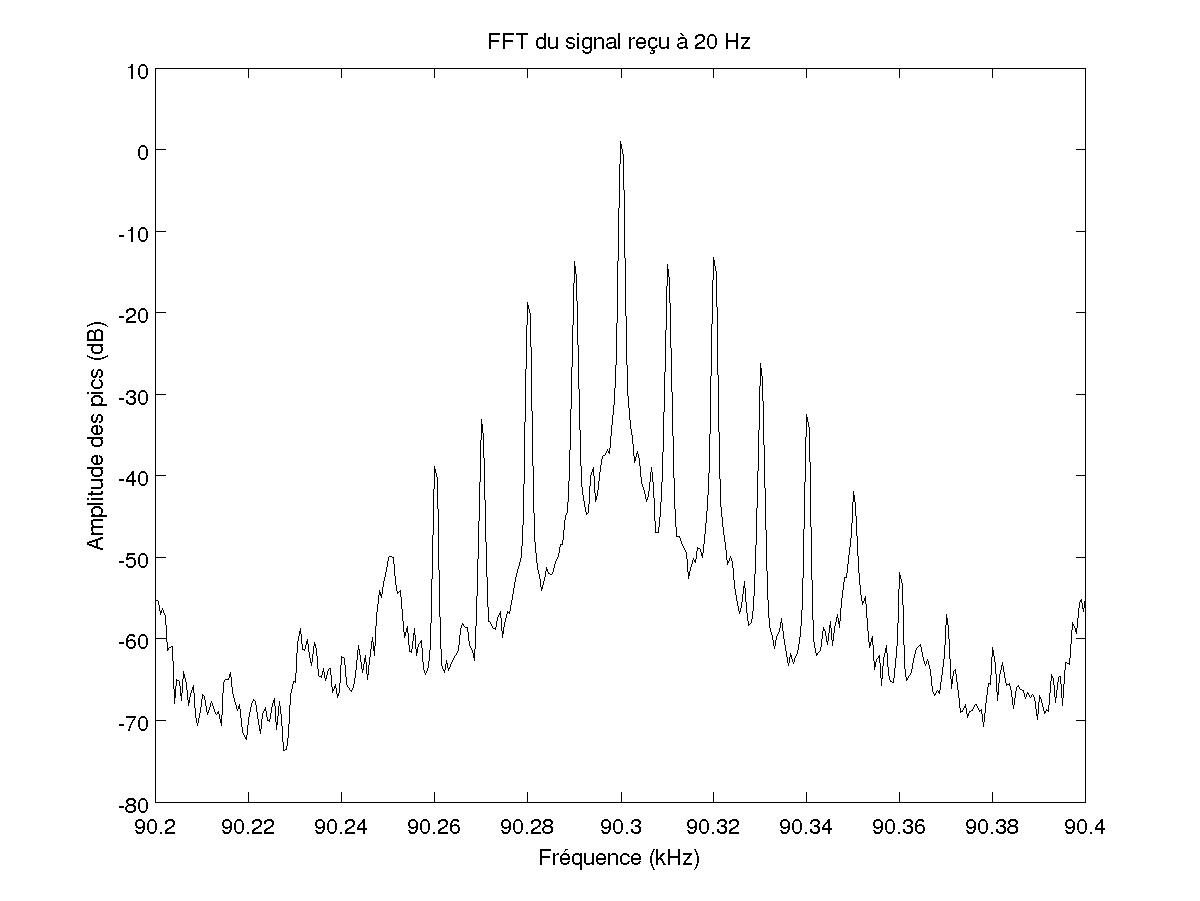
FIG 25 - FFT du signal pour 20 Hz
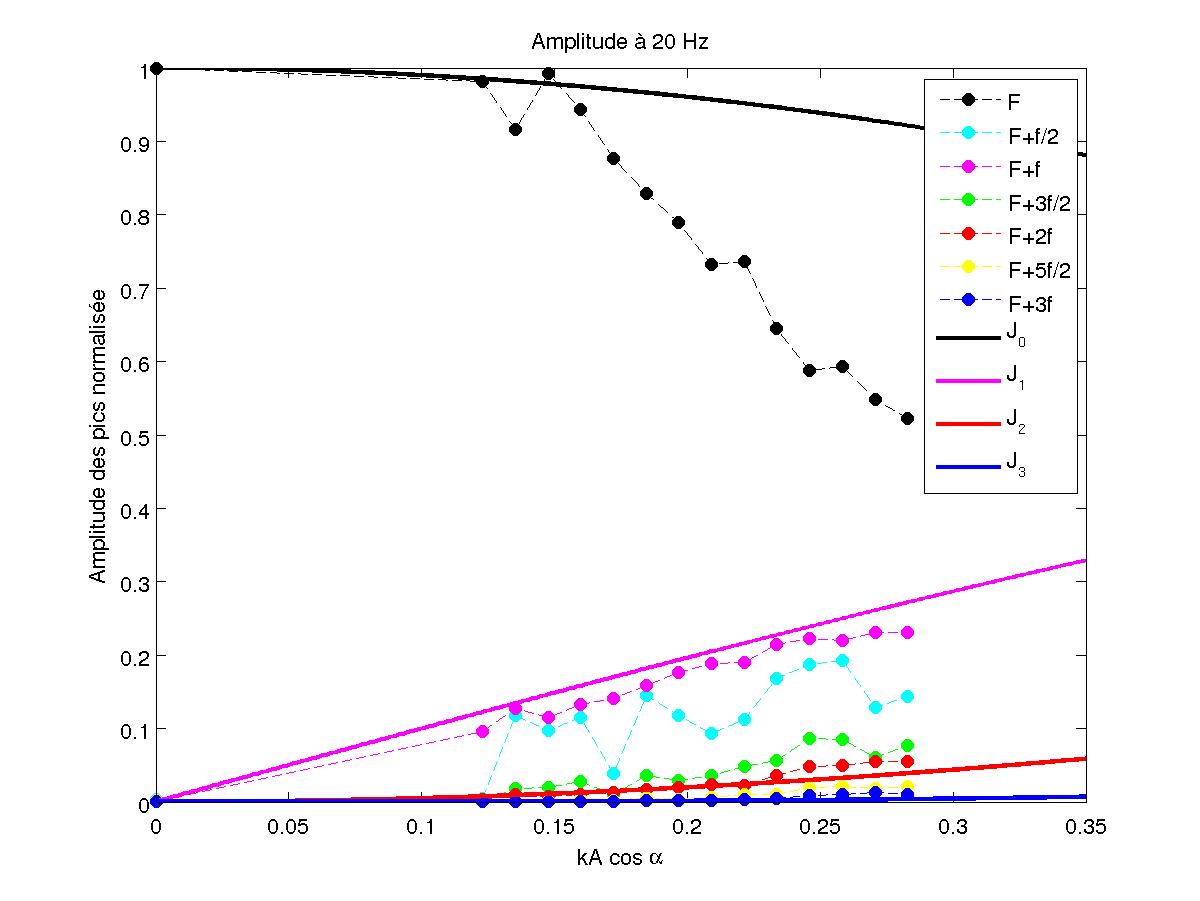
FIG 26 - Amplitude des pics en fonction de kA obtenues pour 20 Hz
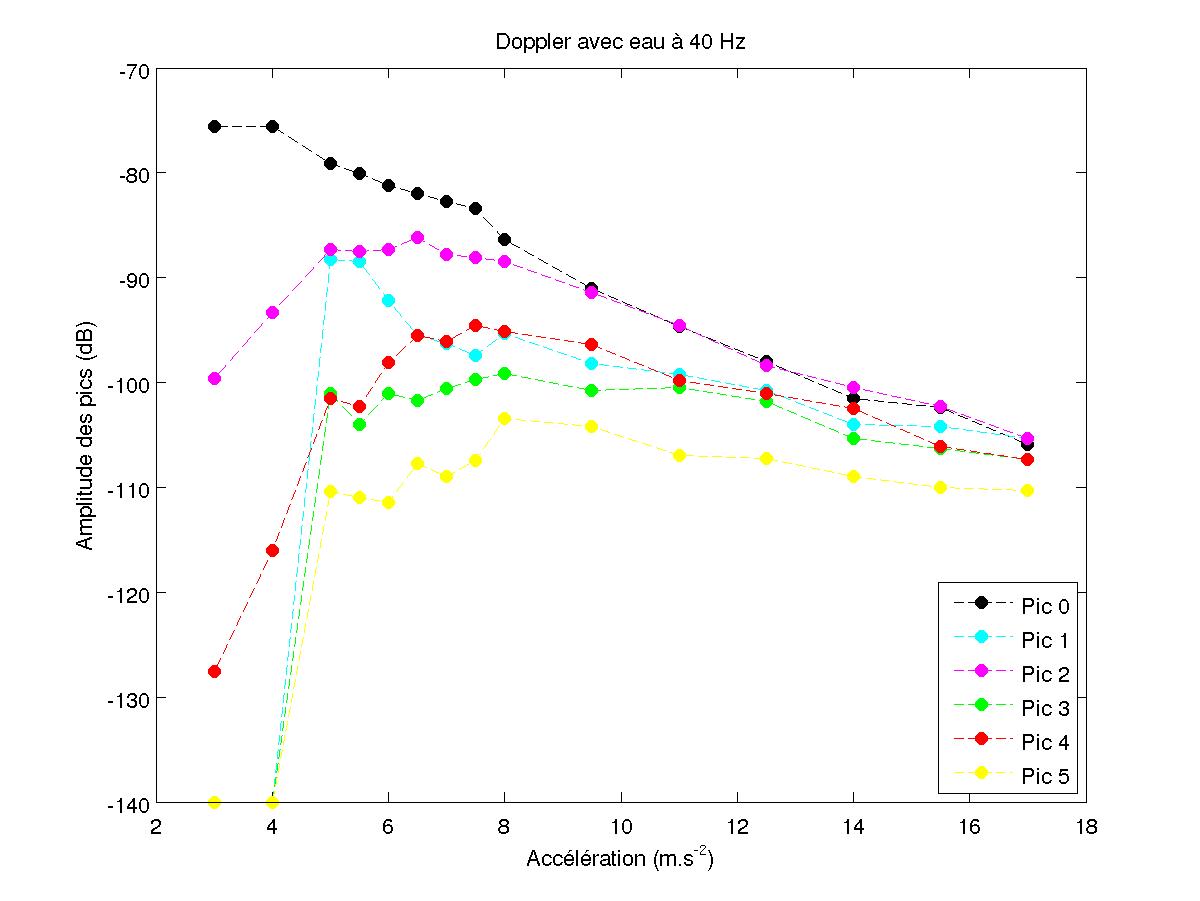
FIG 27 - Amplitude en décibel pour 40 Hz
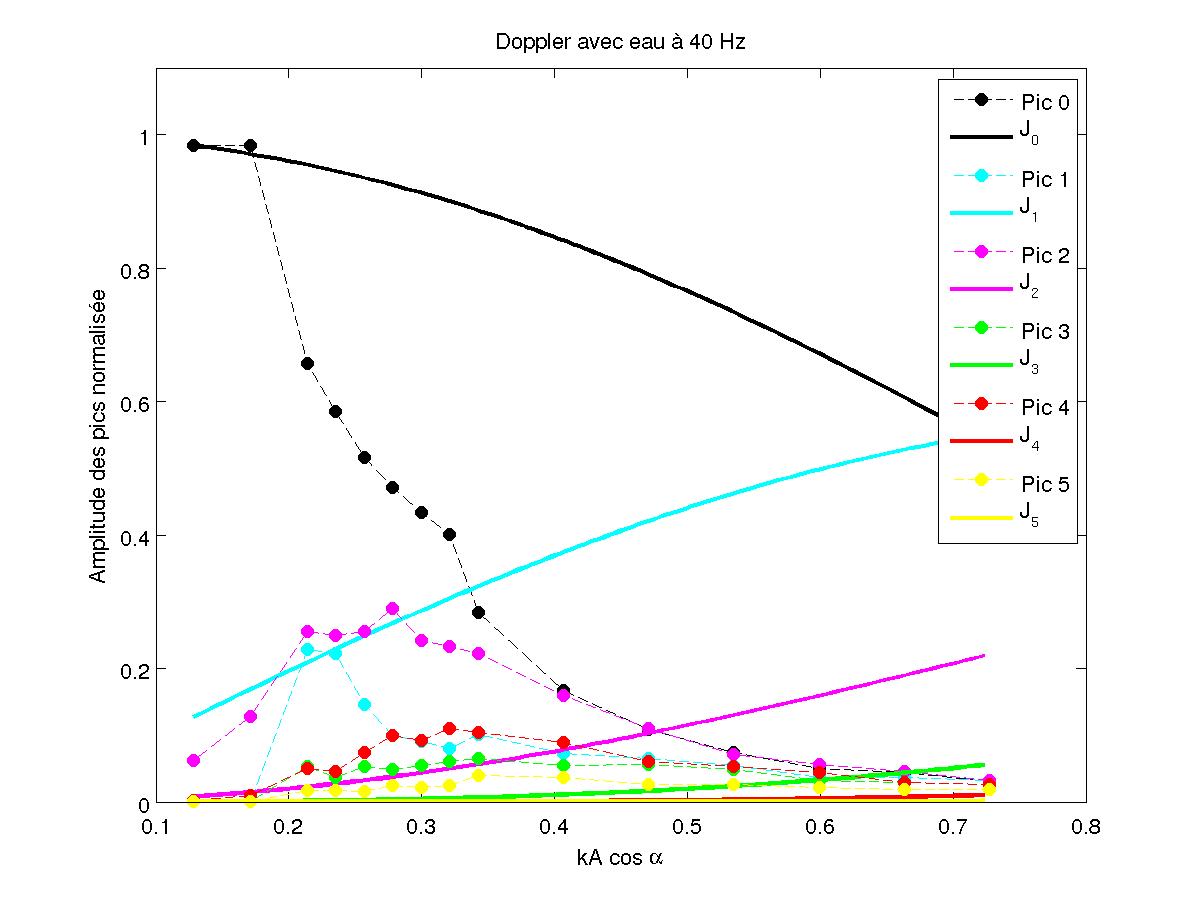
FIG 28 - Amplitude normalisée pour 40 Hz
On voit alors que des pics apparaissent aux fréquences F+nf/2 et notamment aux fréquences moitié contrairement au cas où il n'y a pas d'instabilité (cf paragraphe 3.2). Cela montre que les motifs de l'instabilité ont pour fréquence f/2 (correspondant à la fréquence fondamentale). Les courbes présentées sont toutes réalisées pour F=146.3 kHz et f=40 Hz.
3.5 Comportement de l'amplitude des ondes au voisinage du seuil de l'instabilité de Faraday
3.5.1 Théorie sur la bifurcation super-critique
L'équation de la surface d'eau est $\xi(\vec x,t)=f(\vec x) A(t)$. On a pour équation sur l'amplitude : $\dot A =f(A)=\mu A - A^3$ qui est symétrique pour A → -A. La solution pour A petit est $A=A_0 e^{\mu t}$ et la solution stationnaire est A=0 ou ± √μ avec μ=a-ac.
- Si a<ac : solution stationnaire : A=0, si A est petit : $A=A_0 e^{(a-a_c) t}$ : on obtient une décroissance de l'instabilité.
- Si a>ac : solution stationnaire : A=$ \pm \sqrt{a-a_c}$, si A est petit : $A=A_0 e^{(a-a_c) t}$ : on obtient une croissance de l'instabilité.
3.5.2 Transition du pic central
Pour les bifurcations prises en compte pour le pic central uniquement, si on considère l'amplitude A du piston plus grande que la hauteur h des vagues (kh≪kA≪1), on a $$J_0(2k(A+h))=J_0(2kA)-2k^2 A h $$ en considérant qu'en présence de l'instabilité, l'argument de la fonction de Bessel d'ordre 0 est 2k(A+h). Si A reste proche de l'amplitude critique, h est proportionnel à J0(2k(A+h))-J0(2kA). On trace la différence au carré en fonction de l'accélération, on trouve alors une droite.
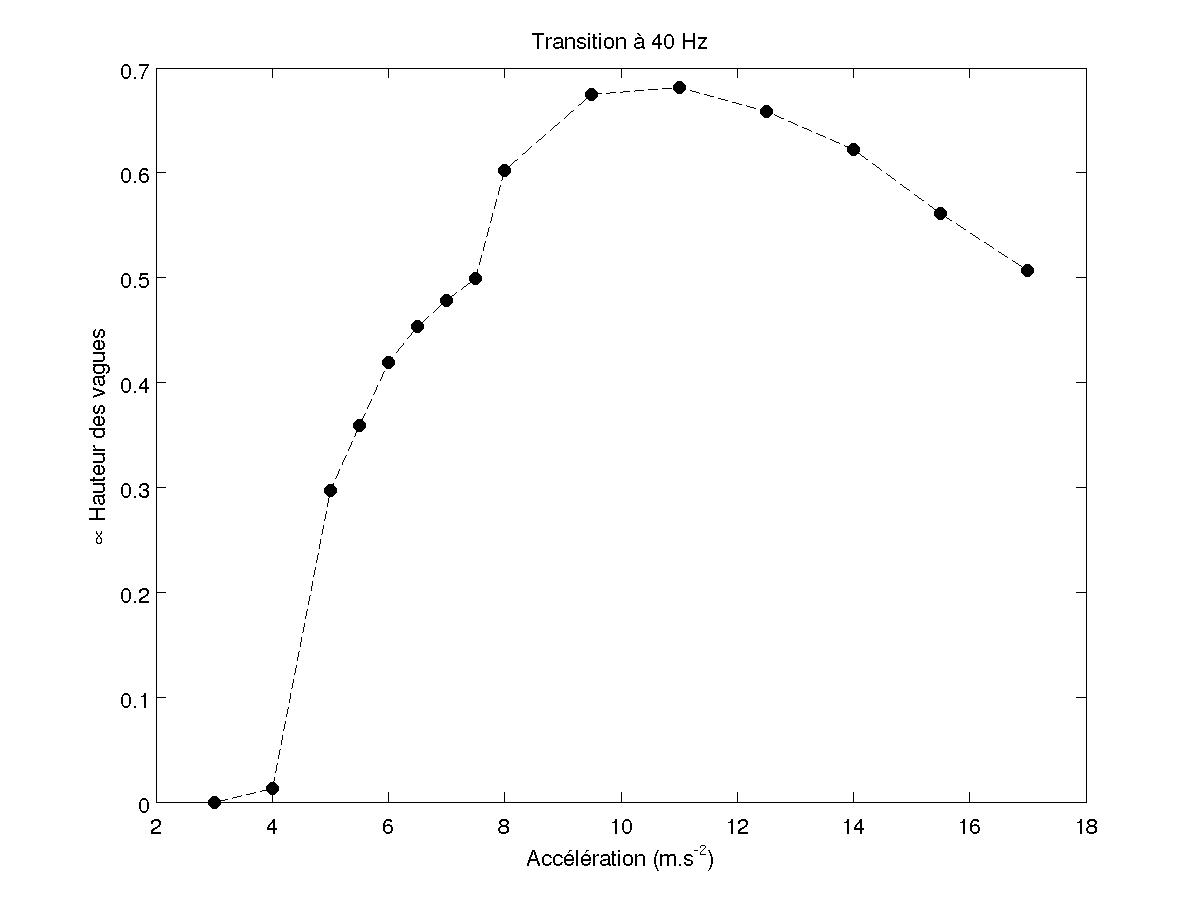
FIG 29 - Transition du pic central pour 40 Hz
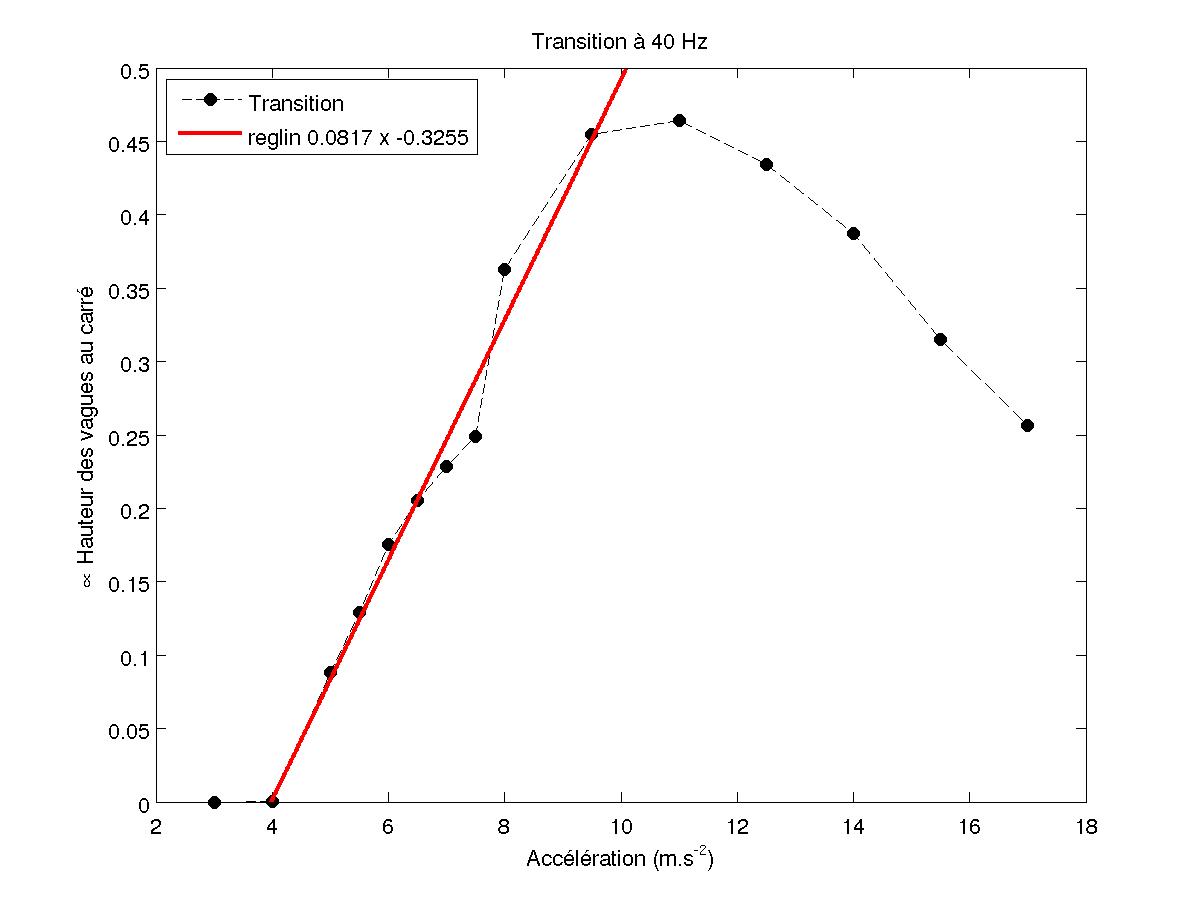
FIG 30 - Transition du pic central pour 40 Hz
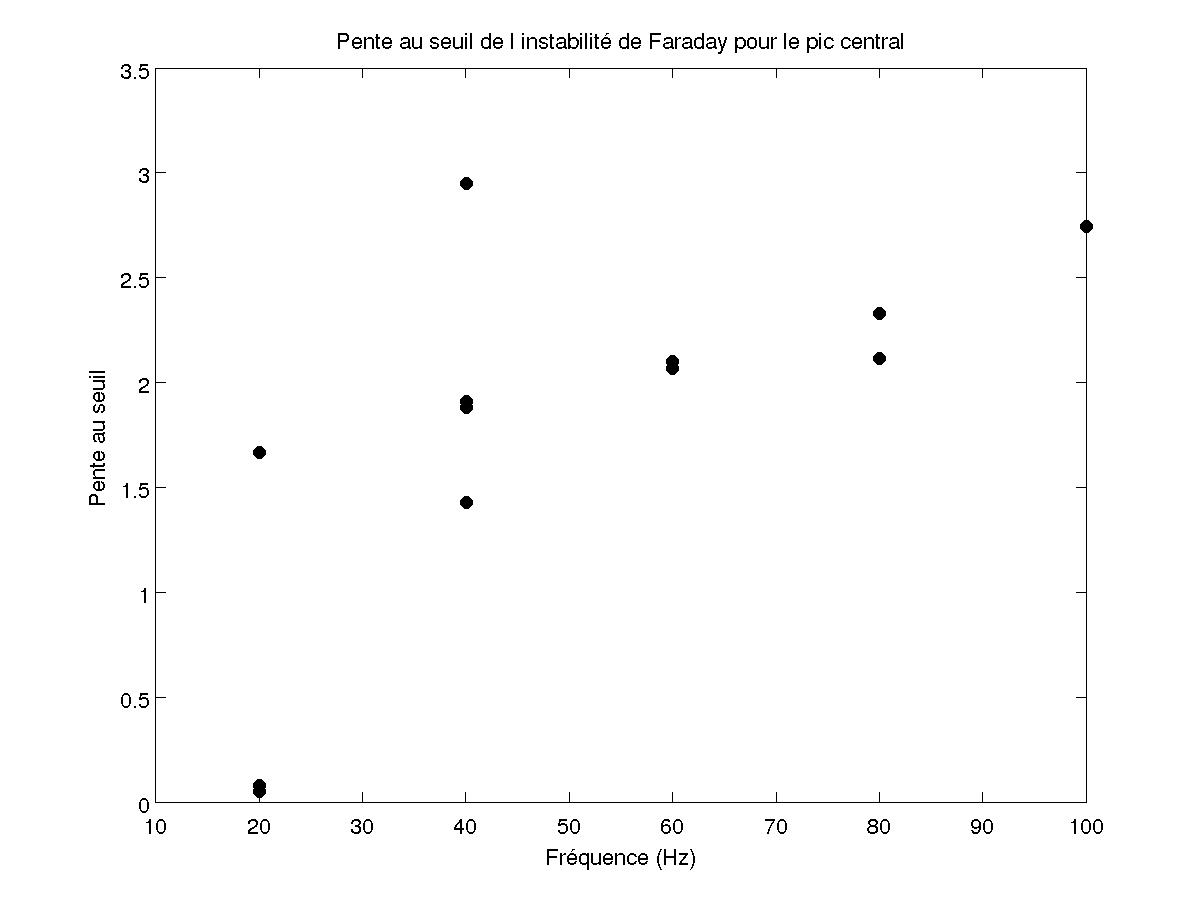
FIG 31 - Pente des transitions en fonction de kA
On essaie également de trouver la hauteur des vagues pour le pic central en inversant la fonction de Bessel d'ordre 0, on obtient alors des courbes similaires aux erreurs de calculs près. En regardant ce qu'il se passe quand on trace la pente de ces courbes en fonction de kA, on remarque que pour le pic central, on obtient une valeur moyenne de 2 pour la majorité des points d'où on obtient que la soustraction de la courbe avec eau par la courbe sans eau égale à $\sqrt{2k(A-A_c)\cos\alpha}$. On observe alors une dépendance en k et en α, ce qui est impossible car la mesure ne change pas la hauteur des vagues, d'où on a une transition, pour A∼Ac, de la forme : $\sqrt{\frac{A-A_c}{A_c}}$ en considérant que tous les termes ne dépendent que du produit 2kA cos α.
3.5.3 Transition des pics secondaires en n.f/2
La variation de l'amplitude des pics à fréquence moitié sont dues uniquement à k et h car ceux-ci n'existent pas avant l'apparition de l'instabilité de Faraday. En inversant les fonctions de Bessel, on obtient alors h en fonction de A (vu que l'on a Jn en fonction de kA) à un coefficient de proportionnalité près. On retrouve des droites comme précédemment.
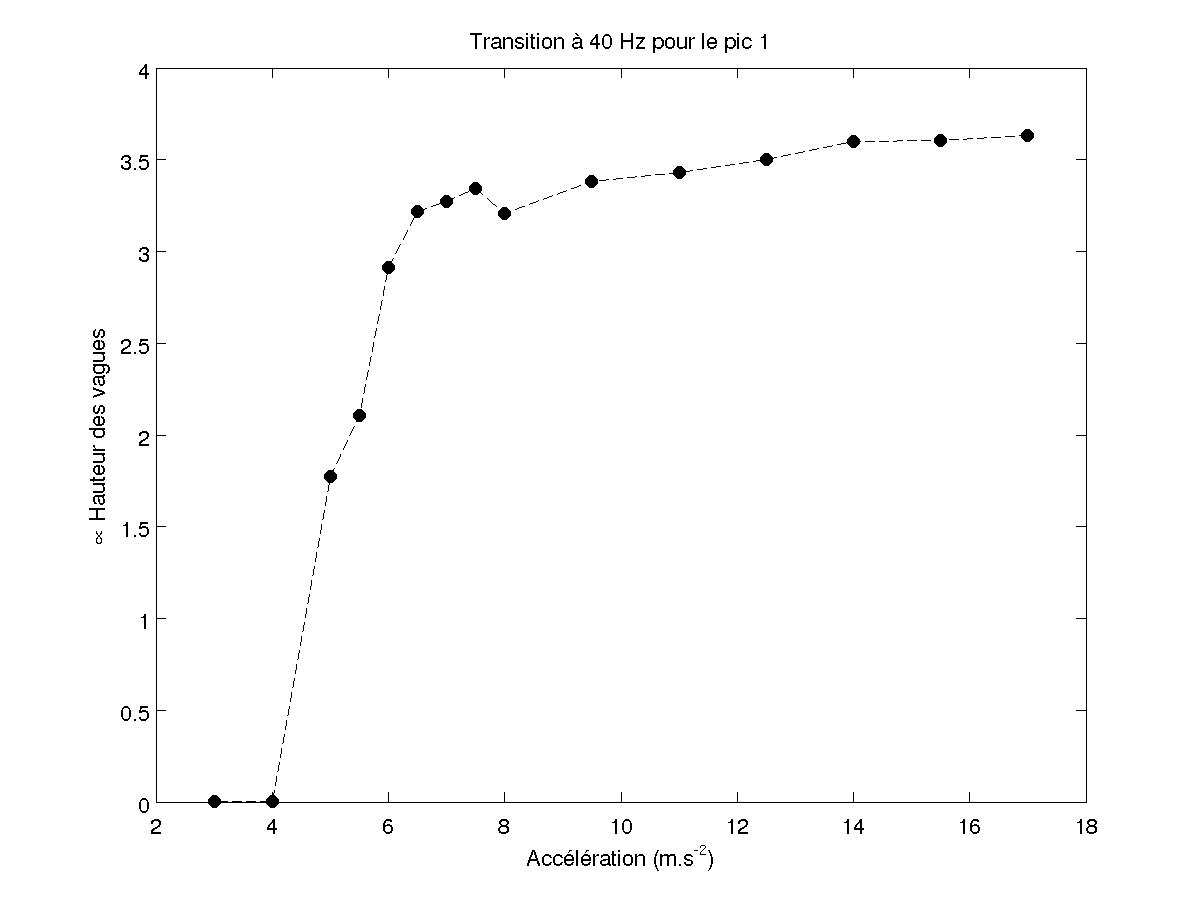
FIG 32 - Transition du pic en f/2 pour 40 Hz
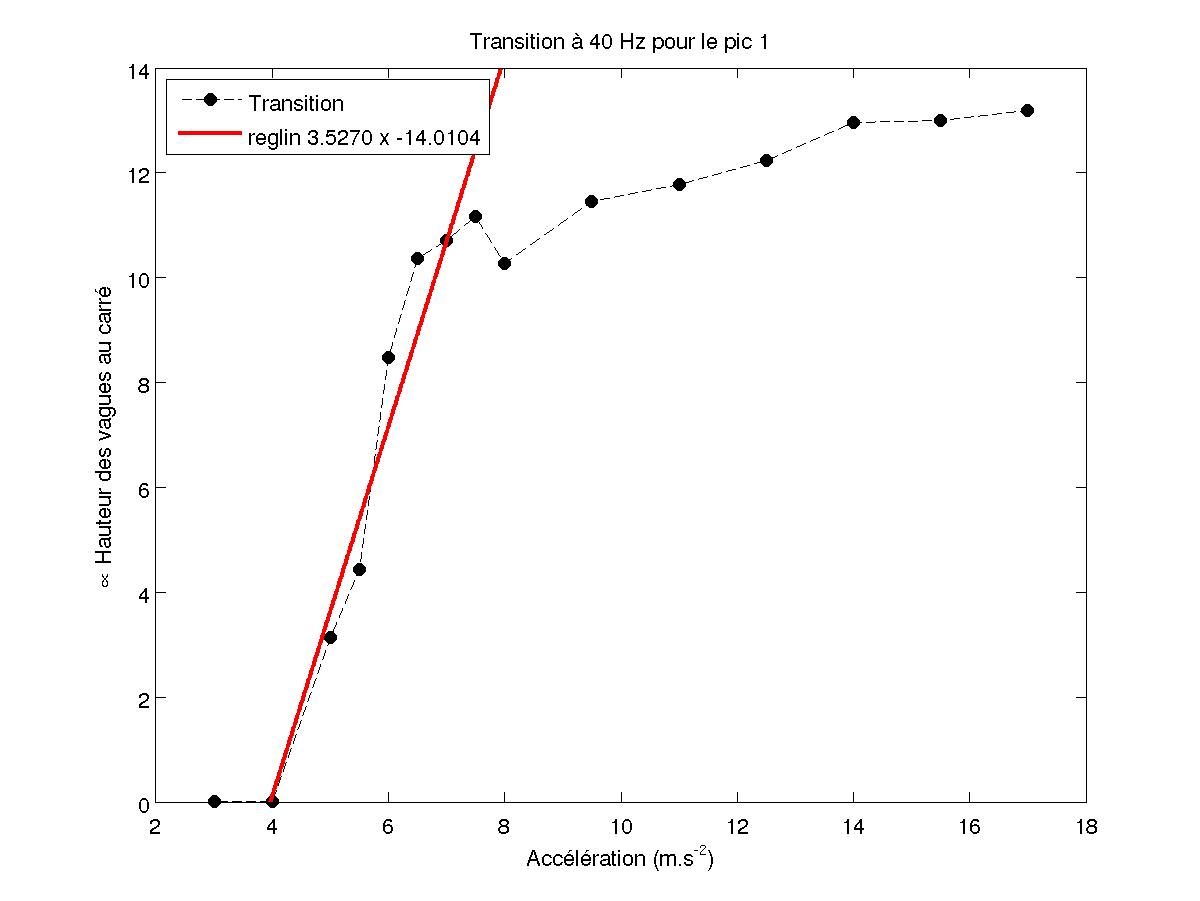
FIG 33 - Transition du pic en f/2 pour 40 Hz
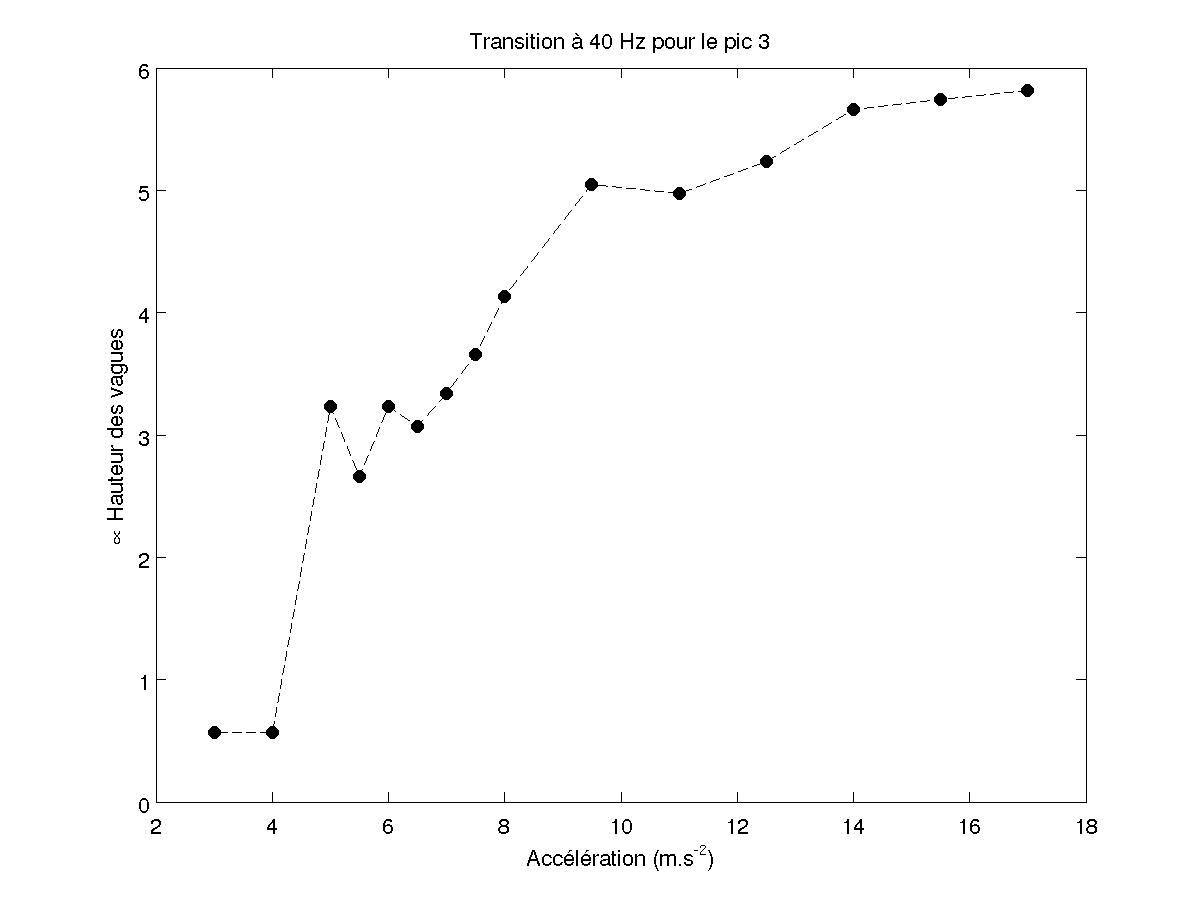
FIG 34 - Transition du pic en 3f/2 pour 40 Hz
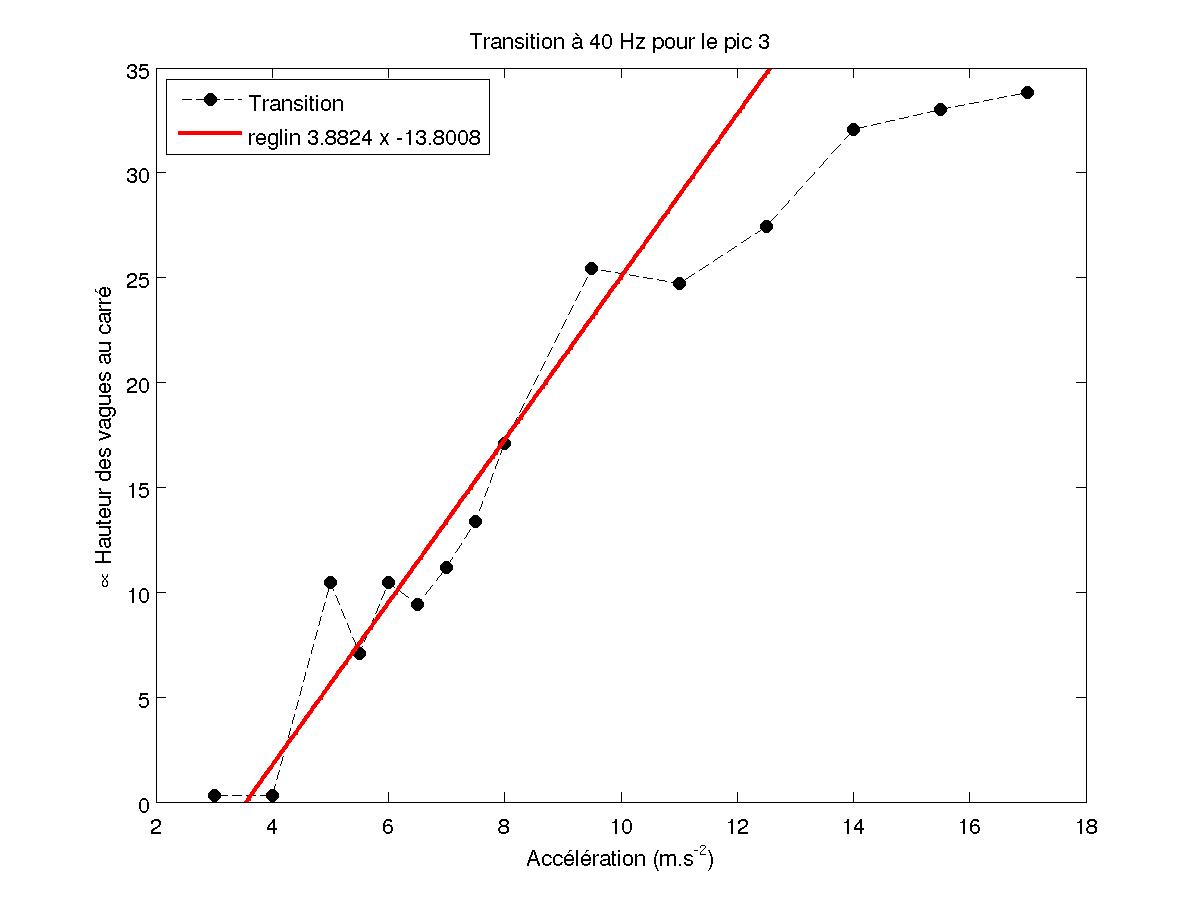
FIG 35 - Transition du pic en 3f/2 pour 40 Hz
3.6 Evolution du seuil de l'instabilité de Faraday avec la fréquence de vibration et comparaison des résultats avec la mesure capacitive
On regarde d'abord l'évolution du seuil en fonction de la fréquence de vibration en reportant l'abscisse à l'origine de toutes les droites obtenues précédemment. On trouve une courbe proche de la théorie. Puis on trace l'évolution de la pente au seuil, en traçant la pente des précédentes droites. En comparant avec la mesure capacitive, on trouve des résultats similaires. On obtient la courbe de l'évolution du seuil en collapsant tous les points à 10 Hz avec la régression de la méthode capacitive pour obtenir l'amplitude des vagues correcte.
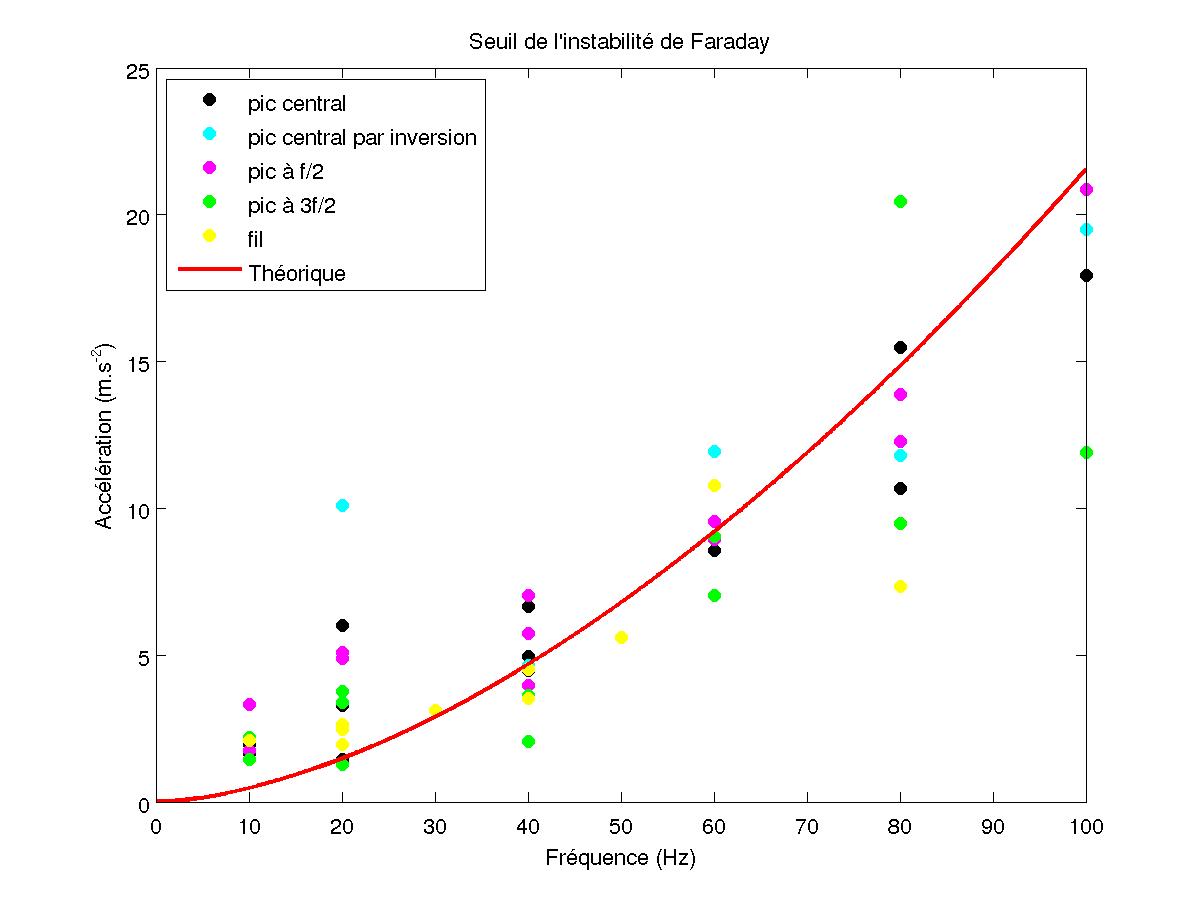
FIG 36 - Evolution du seuil
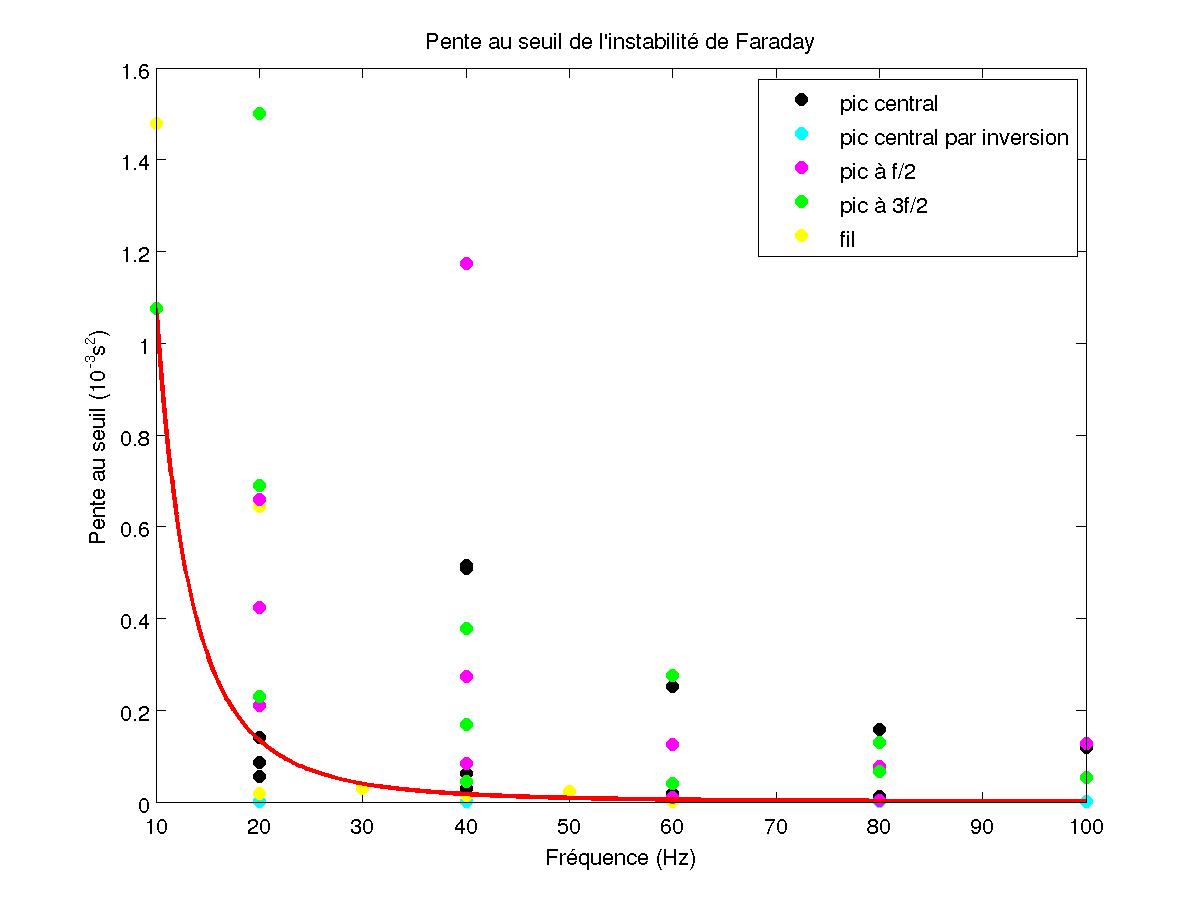
FIG 37 - Evolution de la pente au seuil
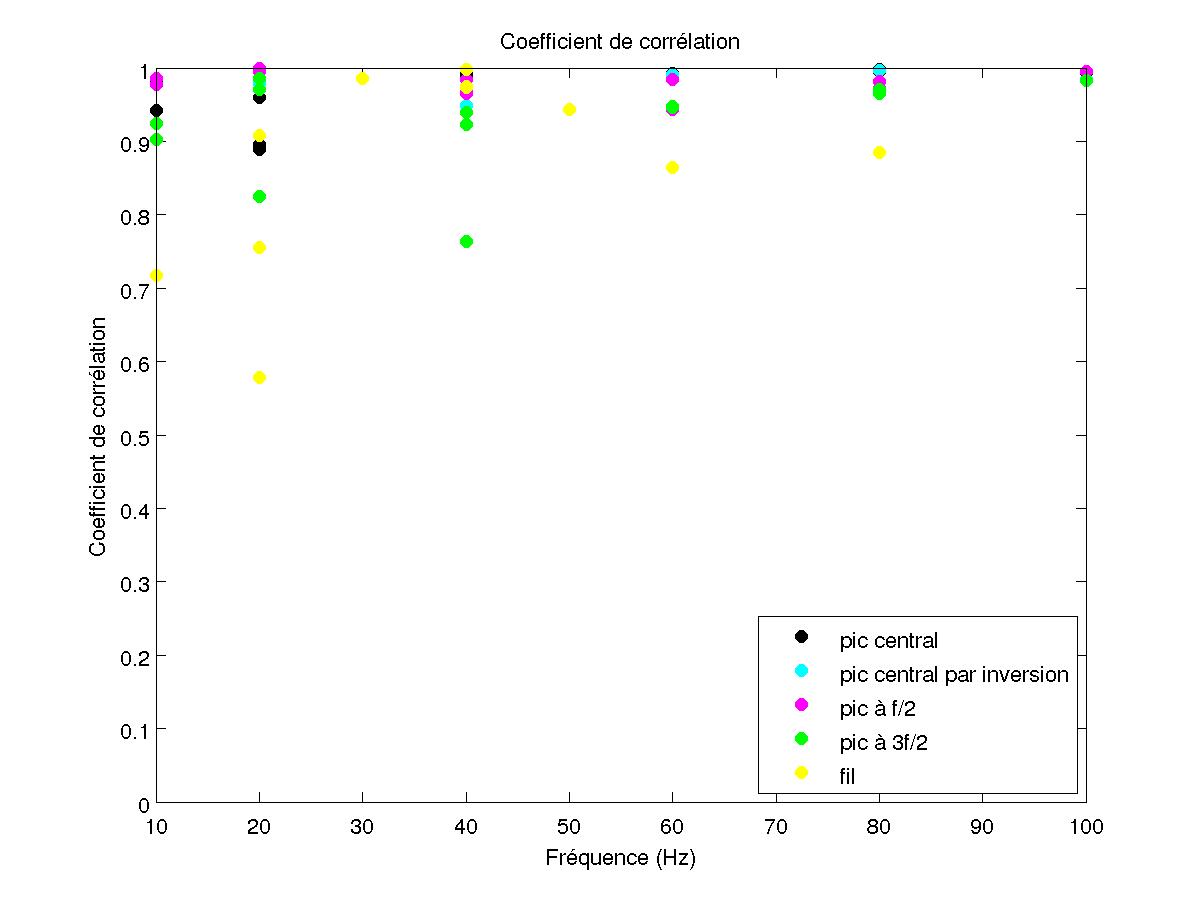
FIG 38 - Coefficients de corrélation
On remarque alors qu'on a toujours une croissance du seuil et une forte décroissance de la pente au seuil de l'instabilité en fonction de la fréquence de vibration. Enfin, les coefficients de corrélation de toutes les droites, reportés sur la figure suivante, montrent que la méthode acoustique (sur le pic central et celui en f/2) obtient un meilleur résultat que la méthode capacitive.
Conclusion
En conclusion, la méthode acoustique permet d'obtenir des résultats similaires, peut-être plus précis, comme le prouve la mesure sans eau où on arrive à reproduire la théorie parfaitement, que la méthode capacitive car il ne s'agit pas d'une mesure locale (il s'agit d'un moyennage sur plusieurs longueurs d'onde) et n'intervenant pas sur le résultat (mesure à distance). On obtient une mesure du seuil de Faraday proche de la théorie avec une croissance en puissance 5/3 et une évolution de la pente au seuil de l'instabilité qui évolue comme 1/f3 avec f la fréquence de vibration de la cuve. Toutes les transitions au seuil sont super-critiques pour la cuve montrant une augmentation du seuil de l'instabilité de Faraday et une décroissance rapide de la pente au seuil de l'instabilité de Faraday en fonction de la fréquence de vibration.
Cependant, les mesures effectuées ont des incertitudes importantes : la mesure capacitive est peu précise à cause de la mesure locale qui dépend fortement de la fluctuation du motif et la mesure acoustique est limitée par le manque de théorie (on ne sait pas s'il s'agit vraiment d'une fonction de Bessel pour une surface ondulée qui vibre ou une fonction proche inconnue dépendant ou non de la fréquence de vibration) qui ne permet pas d'obtenir précisément l'amplitude de l'instabilité et encore à un facteur multiplicatif près. De plus, des mesures optiques ont été faites mais elles ne sont précises que pour des vagues très petites (de pente très faible) sinon la déflexion du faisceau laser est trop grande pour permettre une mesure.
Remerciements
Tout d'abord, je tiens à remercier Stéphan Fauve pour l'aide apportée pendant le stage et pendant la rédaction du rapport ainsi que François Pétrélis et Christophe Gissinger pour leur enseignement sur le sujet de stage et leur disponibilité à n'importe quelle heure de la journée. De plus, je tiens à remercier Claude Laroche, Benoît Semin et Pierre Mourier pour leur présence au laboratoire et leur aide pendant la durée du stage. Enfin, je remercie Nicolas Mujica pour sa venue au laboratoire et son éclaircissement de quelques problèmes.
Bibliographie
[1] R. Wunenburger, N. Mujica, and S. Fauve, Scattering of a sound wave by a vibrating surface, EPJ B 33, 209–213 (2003).
[2] R. Wunenburger, N. Mujica, and S. Fauve, Experimental study of the doppler shift generated by a vibrating scatterer, J. Acoust. Soc. Am. 115, 507–514 (2004).
[3] E.O. LaCasce Jr, and P. Tamarkin, Underwater soung reflection from a corrugated surface, J. Appl. Phys. 27, 138–148 (1956).