Projet de Physique Numérique : Allées de Von Karman (Novembre-Décembre 2013)
Projet réalisé avec Florian Beaugnon
La seconde partie de l'évaluation du cours de physique numérique du Master 1 de l'Ecole Normale Supérieure consiste à coder un problème concret tout en vérifiant la stabilité et la convergence de la solution. Notre projet était basé sur l'étude des allées de Bénard - Von-Kàrmàn qui se apparaissent pour un déplacement de fluide à nombre de Reynolds allant de 10 à 1000 après un obstacle. Les simulations ont été réalisées pour un obstacle immobile, ainsi que mobile avec des mouvements oscillants
Sommaire
1 Position du problème
1.1 Phénomène physique
On place un obstacle sphérique sous un flux de fluide à une vitesse constante U selon l'axe x.
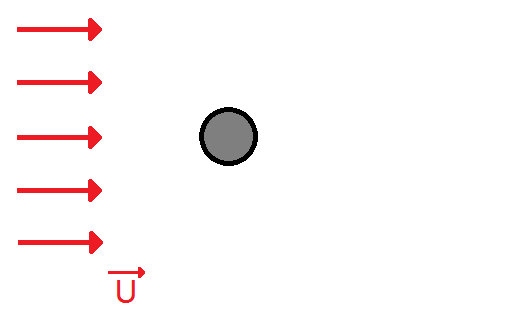
FIG 1 - Schéma du problème
On définit le nombre de Reynolds comme : \[Re=\frac{L.U}{\nu}\] avec L la dimension caractérique de l'obstacle et ν la viscosité dynamique du fluide. Dans l'ensemble du projet, on utilise ν=10-6 m2.s-1, l'ordre de grandeur de la viscosité cinématique de la plupart des fluides. Pour un certain interval de Re, il se crée, après l'obstacle, une couche limite ni laminaire, ni turbulente caractérisant les allées de Von-Kármán.

FIG 2 - Allées de Von-Kármán naturelles
1.2 Equations du problème physique
On suppose que le problème est invariant selon l'axe z, on peut alors négliger l'effet de la gravité dans les équations de la dynamique. Dans ce cas, l'obstacle est un cylindre selon l'axe z. Le fluide est considéré comme incompressible, le mouvement est donc régit par l'équation de Navier-Stokes (1) et l'équation de la conservation de la masse réduite à l'equation (2). $$ \frac{\partial \vec u}{\partial t} + (\vec u . \vec \nabla)\vec u = - \frac{1}{\rho} \vec \nabla P + \nu {\vec \nabla}^2 \vec u \tag{1}$$ $$ \vec \nabla . \vec u = 0 \tag{2}$$
1.3 Equations adimensionnées
On adimensionne les équations (1) et (2) avec les paramètres : L pour les longueurs, U pour les vitesses et ρU2 la pression cinématique, pour la pression. On obtient alors les équations suivantes : $$\frac{\partial \vec u}{\partial t} + (\vec u . \vec \nabla)\vec u = - \vec \nabla \Pi + \frac{1}{R_e} {\vec \nabla}^2 \vec u\tag{3}$$ $$\vec \nabla . \vec u = 0\tag{4}$$
1.4 Equations discrétisées
On discrétise l'équation (3) par une approche semi-lagrangienne : $$ \frac{D \vec u}{D t}=\frac{\partial \vec u}{\partial t} + (\vec u . \vec \nabla)\vec u = \frac{\vec u^{n+1}(\vec x)-\vec u^n(\vec x - \vec u \Delta t)}{\Delta t} \tag{5} $$ En introduisant le vecteur intermédiaire $\vec{u^*}$, on a : $$ \frac{\vec u^{n+1}(\vec x)-\vec u^{*n}}{\Delta t} = - \vec \nabla \Pi^n(\vec x) \tag{6} $$ $$ \frac{\vec u^{*n}-\vec u^n(\vec x - \vec u \Delta t)}{\Delta t}=\frac{1}{R_e} {\vec \nabla}^2 \vec u^n(\vec x) \tag{7}$$ En posant φ=πΔt et en utilisant l'équation (4) à tout temps, $$ \vec u^{*n} =\vec u^n(\vec x - \vec u \Delta t)+\frac{\Delta t}{R_e} {\vec \nabla}^2 \vec u^n(\vec x) \tag{8} $$ $$ {\vec \nabla}^2 \phi^n(\vec x) = \vec \nabla . \vec u^{*n} \tag{9} $$ $$ \vec u^{n+1}(\vec x)=\vec u^{*n}- \vec \nabla \phi^n(\vec x) \tag{10} $$
1.5 Conditions aux limites
Sur les parois libres (en haut, en bas et à droite), on impose $(\vec \nabla . \vec {dS}) \vec u =0$ ainsi que $\vec \nabla P . \vec {dS} =0$. En entrée, on impose la vitesse $\vec u = U \vec x$ et la pression. Dans l'obstacle, on impose une vitesse nulle.
2 Explication du programme
2.1 Différents modes du programme
Notre programme comporte plusieurs modes, choisis à l'aide d'une interface graphique au début du programme, pour l'obstacle, les conditions aux limites et le colorant. Les types d'obstacle (cf la section 2.9) sont les suivants :
- immobile : un obstacle rond est immobile dans le fluide.
- oscillationv : l'obstacle rond oscille verticalement.
- oscillationh : l'obstacle rond oscille horizontalement.
- cercle : l'obstacle rond décrit un cercle.
- propulsion1 : l'obstacle composé bat comme un éventail, et les disques qui le composent ont un mouvement vertical.
- propulsion2 : l'obstacle composé bat comme un éventail, et les disques qui le composent décrivent des arcs de cercle.
Les modes de conditions aux limites (cf la section 2.8) sont les suivants :
- avec : deux plaques horizontales fixent la vitesse du fluide zéro le long des parois haute et basse.
- sans : la vitesse du fluide est libre sur ces plaques.
- propulsion : il y a les mêmes plaques que pour le mode 'avec' et la pression est libre le long de la paroi d'entrée.
Les modes de colorant (cf la section 2.2) sont les suivants :
- ligne : le colorant est introduit le long d'une ligne sur toute la longueur de la paroi d'entrée du fluide dans le domaine.
- barres : le colorant est introduit sur plusieurs segments répartis sur la paroi d'entrée.
- points : le colorant est introduit sur plusieurs points répartis sur la paroi d'entrée du fluide.
- obstacle : le colorant est introduit le long d'un segment un peu plus large que l'obstacle le long de la paroi d'entrée du fluide, face à l'obstacle.
- tirets : le colorant est introduit le long de deux petits segments le long de la paroi d'entrée du fluide, de part et d'autre de l'obstacle.
2.2 Colorant
Le colorant est un scalaire passif compris entre 0 et 1 qui ne se propage que par advection et qui permet donc de suivre le déplacement d'une particule fluide. Il peut être introduit de deux manières : soit en fixant sa valeur, soit en fixant une valeur initiale à 1 dans tout le domaine, et le fluide entrant se colore.
def Colorant(mode,N=8): global c,NY if mode=='ligne': c[:,1]=1. elif mode=='points': for i in range(N): c[int((i+0.5)*NY/N),1]=1. elif mode=='barres': for i in range(N): c[int((2*i+0.5)*NY/(2*N)):int((2*i+1.5)*NY/(2*N)),1]=1. elif mode=='obstacle': c[int(3*NY/7):int(4*NY/7),1]=1. elif mode=='tirets': c[int(3*NY/8)-2:int(3*NY/8)+2,1]=1. c[int(5*NY/8)-2:int(5*NY/8)+2,1]=1.
Lorsque tout le domaine est coloré, on peut suivre la traînée de l'obstacle à cause de la diffusion entre le fluide coloré et l'obstacle incolore, qui a pour effet de décolorer le fluide ayant été en contact avec l'obstacle, qui lui-même ne se colore pas car on impose son taux de colorant à chaque itération.
2.3 Définition des opérateurs
Laplacien
Le laplacien 1D discrétisé à l'ordre 2 donne : $$\frac{\partial^2 v}{\partial x^2} = \frac{v_{k+1}-2 v_k + v_{k-1}}{dx^2} $$ On a alors pour le laplacien 2D (avec i correspondant à la variable y et j à la variable x) : $$\Delta v = \frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} = \frac{v_{i,j+1}-2 v_{i,j} + v_{i,j-1}}{dx^2} + \frac{v_{i+1,j}-2 v_{i,j} + v_{i-1,j}}{dy^2}$$
def Laplacien(v): global NX,NY,dx_2,dy_2 lapv=np.empty((NY,NX)) coef0=-2*(dx_2+dy_2) lapv[1:-1,1:-1]=(v[1:-1,2:]+v[1:-1,:-2])*dx_2+(v[2:,1:-1]+v[:-2,1:-1])*dy_2+v[1:-1,1:-1]*coef0 return lapv
Divergence
La divergence 2D discrétisée à l'ordre 2 (avec i correspondant à la variable y et j à la variable x) donne : $$\vec \nabla. \vec v = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = \frac{u_{i,j+1}-u_{i,j-1}}{2dx} + \frac{v_{i+1,j}-v_{i-1,j}}{2dy}$$
def divergence(u,v): global NX,NY,dx,dy divv=np.empty((NY,NX)) divv[1:-1,1:-1]=(u[1:-1, 2:]-u[1:-1, :-2])/(2*dx)+(v[2:, 1:-1]-v[:-2, 1:-1])/(2*dy) return divv
Gradient
Le gradient 2D discrétisé à l'ordre 2 (i correspondant à la variable y et j à la variable x) donne : $$\vec \nabla f= \frac{\partial f}{\partial x} \vec x + \frac{\partial f}{\partial y} \vec y = \frac{f_{i,j+1}-f_{i,j-1}}{2dx}\vec x + \frac{f_{i+1,j}-f_{i-1,j}}{2dy} \vec y$$
def grad(f): global NX,NY,dx,dy gradfx=np.empty((NY,NX)) gradfy=np.empty((NY,NX)) gradfx[:,1:-1]=(f[:,2:]-f[:,:-2])/(dx*2) gradfy[1:-1,:]=(f[2:,:]-f[:-2,:])/(dy*2) return [gradfx,gradfy]
2.4 Calcul du pas de temps
On calcule à chaque pas de temps le nouveau dt correspondant à la condition d'advection : $|\vec v|dt$ doit être inférieur au pas de la grille,
def CFL_advection(): """Condition CFL Advection qui retourne le nouveau 'dt' tel que abs(V)*dt<dx""" global u,v,dx,dy precautionADV=1. umax=max(np.abs(u).max(),0.01) vmax=max(np.abs(v).max(),0.01) dt_cfa=precautionADV*min(dx/umax,dy/vmax) return dt_cfa
et à la condition de stabilité du schéma diffusif 1D : $dt<\frac{dx^2}{4D}$ avec D le coefficient de diffusivité.
def CFL_explicite(): """Condition CFL pour la diffusion en cas de schema explicite""" global DeltaU,dx,dy precautionEXP=0.3 dt_DeltaU_x=dx**2/(4.*DeltaU) dt_DeltaU_y=dy**2/(4.*DeltaU) dt_cfl=precautionEXP*min(dt_DeltaU_x,dt_DeltaU_y) return dt_cfl
Le dt choisit est donc le minimum de ces deux valeurs.
dt_exp=CFL_explicite() dt_adv = CFL_advection() dt_new = min(dt_adv,dt_exp) if (dt_new < dt): dt = dt_new t+=dt
2.5 Étape d'advection
L'étape d'advection permet de calculer le terme $u^n(\vec x - \vec u \Delta t)$ de l'équation (8) ainsi que le terme $c^{n+1}=c^n(\vec x - \vec u \Delta t)$ du scalaire passif. On appelle alors [Resu,Resv,Resc] les quantités [u,v,c] advectées de $\vec v dt$.
Ordre 1
L'advection est calculée pour u, v et c et pour tous les points réels. On a donc pour un champ scalaire, $$v_{advecté}=\sum_{i,j \in quadrant} \frac{A_{i,j}}{A_{quadrant}}v_{i,j}$$ Le programme calcule tout d'abord dans quel quadrant le champ advecté se trouve, puis calcule sa valeur en moyennant sur les valeurs situées aux coins de celui-ci.
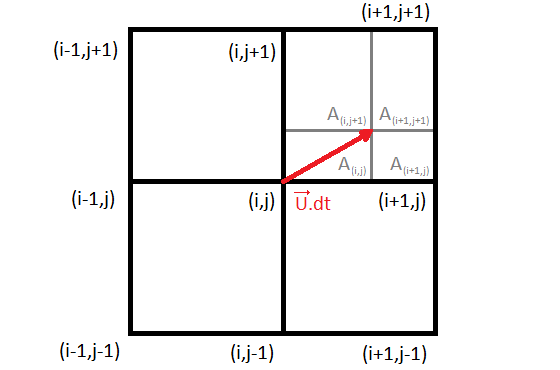
FIG 3 - Schéma d'advection
Ordre 2
Le schéma d'advection à l'ordre 1 est diffusif (figure 4), ce qui n'est pas gênant pour la vitesse car négligeable devant le terme de diffusion « réelle ». Le colorant en revanche gagne à être plus net. On peut réduire cette diffusion grâce à un schéma d'advection à l'ordre 2 (figure 5) : après une la première étape d'advection, on réadvecte le résultat obtenu en sens inverse. Dans une situation idéale le résultat obtenu serait identique, et la moyenne entre ces deux valeurs correspond à la diffusion causée par l'étape d'advection. On retranche donc celle-ci au résultat de l'advection à l'ordre 1. On a donc, d'après [1], le champ scalaire advecté par la formule suivante $$\phi^{n+1}=L(\vec u, \phi^n + \frac{1}{2}(\phi^n - \bar{\phi}))$$ où $\bar{\phi}=L(-\vec u, L(\vec u,\phi^n))$ et L correspond au schéma d'advection d'ordre 1.
Correction de l'ordre 2
def Advect2(u,v,c,D=0.3): Resu1=Advect(u,v,u)[2] Resv1=Advect(u,v,v)[2] Resc1=Advect(u,v,c)[2] GhostPoints(Resu1);GhostPoints(Resv1);GhostPoints(Resc1) Resu2=u+0.5*(u-Advect(-u,-v,Resu1)[2]) Resv2=v+0.5*(v-Advect(-u,-v,Resv1)[2]) Resc2=c+D*(c-Advect(-u,-v,Resc1)[2]) GhostPoints(Resu2);GhostPoints(Resv2);GhostPoints(Resc2) return Advect(Resu2,Resv2,Resc2)
Ce schéma du second ordre corrige en grande partie la diffusion mais fait apparaitre de la dispersion numérique, c'est-à-dire des lignes alternées colorées/non colorées qui se propagent près des discontinuités dans la concentration en colorant. Pour éviter ces lignes, on revient vers le premier ordre en changeant le coefficient du terme d'ordre 2 (0.3 au lieu de 0.5), ce qui a pour effet de réintroduire de la diffusion et donc de limiter la formation des lignes (figure 7).
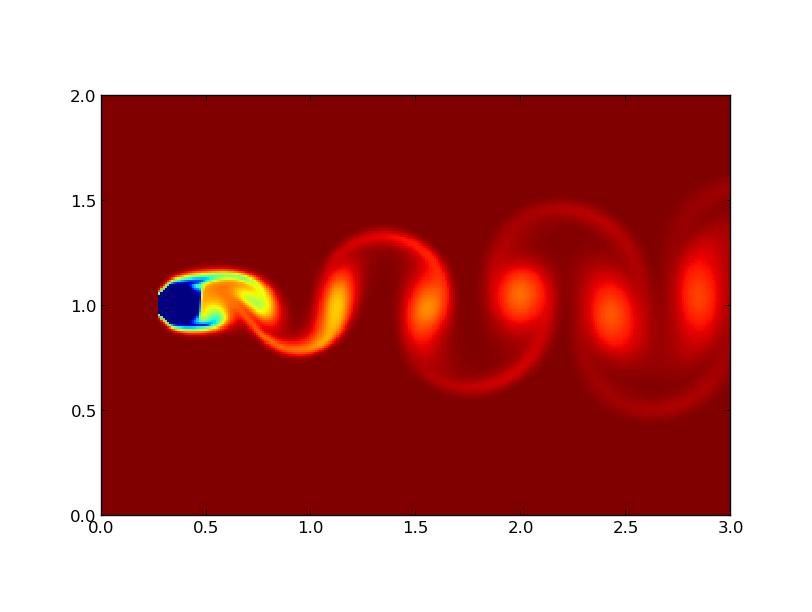
FIG 4 - Schéma d'ordre 1
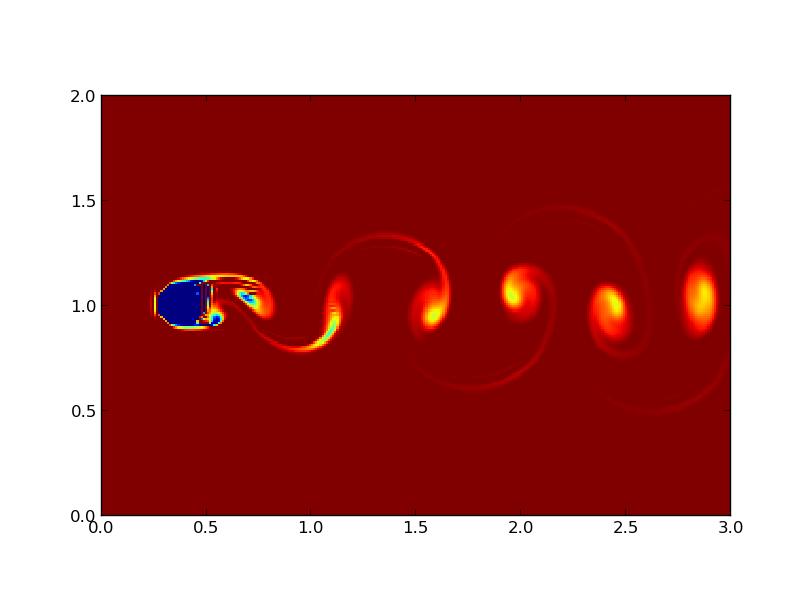
FIG 5 - Schéma d'ordre 2
2.6 Étape de diffusion
Cette étape permet de calculer la vitesse $\vec u^{*n}$ à partir de l'équation (8).
ustar = Resu + dt*Laplacien(u)/Re vstar = Resv + dt*Laplacien(v)/Re
2.7 Étape de projection
L'étape de projection permet tout d'abord de calculer $\phi^n(\vec x)$ en inversant l'équation (9) : on calcule la divergence de $\vec u^{*n}$ et on inverse l'équation de Laplace grâce à la fonction ResoLap. Dans un second temps, on obtient la vitesse $\vec u^{n+1}$ grâce à l'équation (10).
divstar=divergence(ustar,vstar) phi[1:-1,1:-1]=ResoLap(LUPoisson,divstar[1:-1,1:-1]) GhostPoints(phi) u=ustar-grad(phi)[0] v=vstar-grad(phi)[1]
2.8 Conditions aux limites et points fantômes
Nous avons utilisés deux scénari pour les conditions aux limites : avec ou sans plaques en haut et en bas du domaine. Dans les deux cas, la condition sur la face de sortie est libre : les dérivées des vitesses u et v sont nulles : $v[:,-2]=v[:,-4]$ En l’absence de plaques, les dérivées des vitesses sont nulles, ce qu'on réalise de la même manière que précédement. Pour représenter des plaques, on se contente d'imposer une valeur nulle pour les vitesses.
def ConditionLimites(u,v): if typeCL=='avec_plaque': u[:,1]=1.; v[:,1]=0. u[:,-2]=u[:,-4]; v[:,-2]=v[:,-4] u[-2,:]=0.; v[-2,:]=0. u[1,:]=0.; v[1,:]=0. elif typeCL=='sans_plaque': u[:,1]=1.; v[:,1]=0. u[:,-2]=u[:,-4]; v[:,-2]=v[:,-4] u[-2,:]=u[-4,:]; v[-2,:]=v[-4,:] u[1,:]=u[3,:]; v[1,:]=v[3,:] elif typeCL=='propulsion': u[:,1]=u[:,3]; v[:,1]=v[:,3] u[:,-2]=u[:,-4]; v[:,-2]=v[:,-4] u[-2,:]=0.; v[-2,:]=0. u[1,:]=0.; v[1,:]=0.
On met des points fantômes nécessaires pour calculer le laplacien, la divergence et le gradient d'une quantité, avec des conditions de Neumann.
def GhostPoints(a): a[:,0]=a[:,2] a[:,-1]=a[:,-3] a[0,:]=a[2,:] a[-1,:]=a[-3,:]
2.9 Obstacle
L'obstacle est constitué d'une zone du fluide où l'on impose la vitesse. Pour étudier les allées avec un obstacle immobile, il suffit d'imposer une vitesse nulle dans une zone fixe. Pour les obstacles mobiles, en revanche, nous avons fixé dans la zone de l'obstacle une vitesse du fluide égale à la vitesse de l'obstacle, ce qui reproduit le comportement en vitesse de la couche directement en contact avec un objet solide en mouvement.
def Obstacle(mode,N=8,w=5.): global NX,NY,dx,dy,L Fu=np.zeros((NY,NX)) Fv=np.zeros((NY,NX)) Fc=np.ones((NY,NX)) if mode=='immobile': Fu,Fv,Fc=Forme(int(NX/8),int(NY/2)) elif mode=='oscillationv': Fu,Fv,Fc=Forme(int(NX/8),int(NY/2+NY/4*np.cos(w*t)),v=-NY*dy/4*w*np.sin(w*t)) elif mode=='oscillationh': Fu,Fv,Fc=Forme(int(NX/4+NY/8*np.cos(w*t)),int(NY/2),u=-NY*dy/8*w*np.sin(w*t)) elif mode=='propulsion1': for i in range(N): a,b,c=Forme(int(NX/8+i*L/(4*dx)),int(NY/2+i*L/(4*dy)*np.cos(w*t)),v=-i*L/4*w*np.sin(w*t)) Fu=Fu*c+a Fv=Fv*c+b Fc*=c elif mode=='propulsion2': for i in range(N): a,b,c=Forme(int(NX/8+i*L/(4*dy)*np.sqrt((np.sin(w*t-np.pi/2)**2+1)/2)), int(NY/2+i*L/(4*dx)*np.sqrt(2)/2*np.cos(w*t-np.pi/2)), u=i*L*dx/(4*dy)*w*np.sin(2*w*t-np.pi)/4*np.sqrt(2/(np.sin(w*t-np.pi/2)**2+1)), v=-i*L*dy/(4*dx)*w*np.sqrt(2)/2*np.sin(w*t-np.pi/2)) Fu=Fu*c+a Fv=Fv*c+b Fc*=c return Fu,Fv,Fc,w
Nous avons utilisé des obstacles ronds. Pour les obstacles battants, plutôt que de chercher à mettre en place un rectangle en rotation nous avons utilisé plusieurs disques alignés et chacun en mouvement selon un arc de cercle. Pour calculer les valeurs de u,v et c dans l'obstacle on utilise trois matrices : Fu, Fv et Fc. Fu et Fv sont des matrices de même dimension que notre domaine, nulles partout sauf dans l'obstacle où elles ont pour valeur les vitesses horizontale et verticale de l'obstacle. La matrice Fc est de même dimension et vaut 1 partout sauf dans l'obstacle où elle est nulle. On obtient alors les valeurs de u, v et c.
def Forme(ctrx,ctry,u=0,v=0): global NX,NY,dx,dy,L Fc=np.ones((NY,NX)) Fu=np.zeros((NY,NX)) Fv=np.zeros((NY,NX)) for i in range(ctry-int(L/dy),ctry+int(L/dy)+1): for j in range(ctrx-int(L/(2*dx)),ctrx+int(L/(2*dx))+1): if np.sqrt(((i-ctry)*dy)**2+((j-ctrx)*dx)**2) < L/2: Fc[i,j]=0. Fu[i,j]=u Fv[i,j]=v return Fu,Fv,Fc ConditionLimites(u,v) u=u*Fc+Fu; v=v*Fc+Fv; c*=Fc
3 Différents résultats avec un écoulement global U=1
3.1 Obstacle immobile
Lorsque l'on utilise un obstacle fixe avec un nombre de Reynolds supérieur à 102, on voit d'abord se créer une perturbation symétrique derrière l'obstacle qui grandit avant d'évoluer en allées de Von Kármán (figure 7). En revanche, si le nombre de Reynolds est inférieur à 102, les allées n'apparaissent pas car l'écoulement reste laminaire (figure 6). Ces observations sont conformes à la réalité physique (section 1).
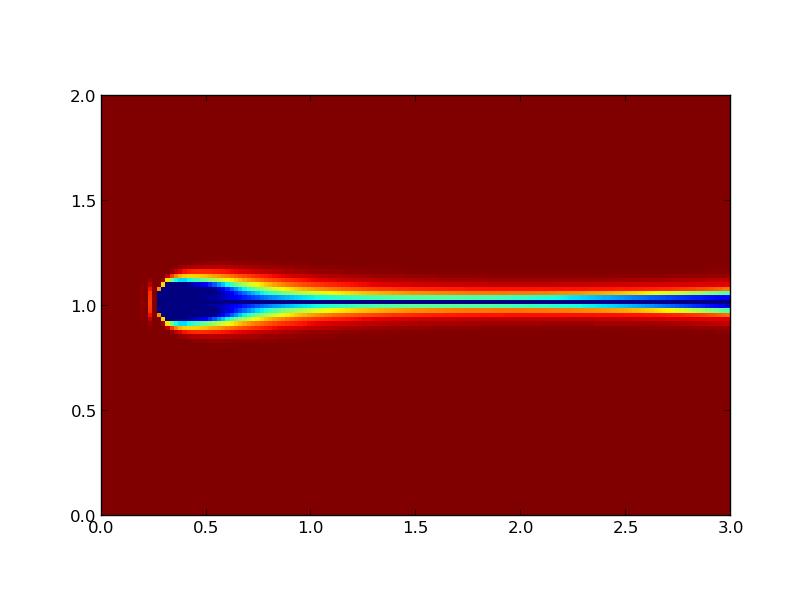
FIG 6 - Obstacle immobile pourRe=102
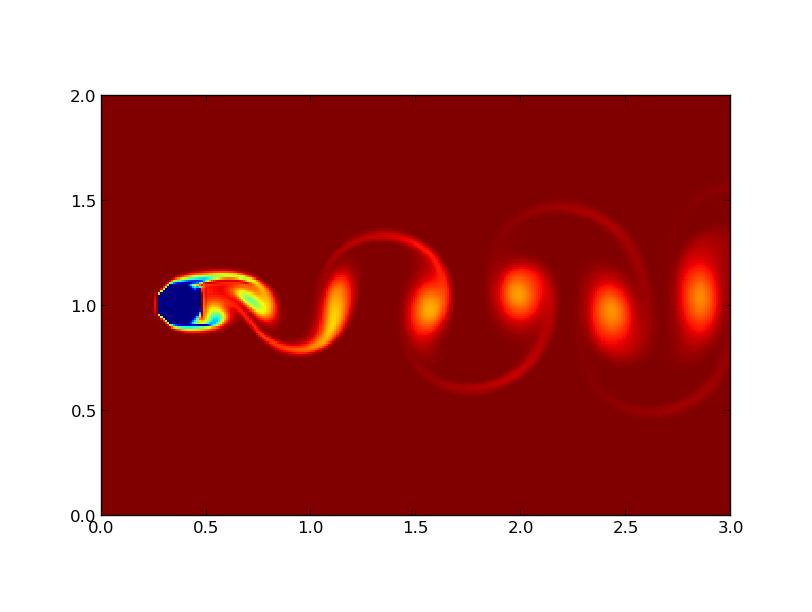
FIG 7 - Obstacle immobile pour Re=103
Dans la suite toutes les figures sont réalisées pour L=0.2 m et U=5.10-3 m.s-1, c'est-à-dire pour un Reynolds de 103. Pour un Reynolds supérieur, des phénomènes de crise de traînée se produisent (normalement l'écoulement devient turbulent à ce moment-là mais comme les phénomènes des petites échelles ne sont pas présents, ce n'est pas le cas ici).
3.2 Obstacle oscillant
On peut aussi utiliser un obstacle oscillant orthogonalement à l'écoulement (figure 8) ou suivant l'écoulement (figure 9), auquel cas on observe aussi des allées, mais avec une forme différente.
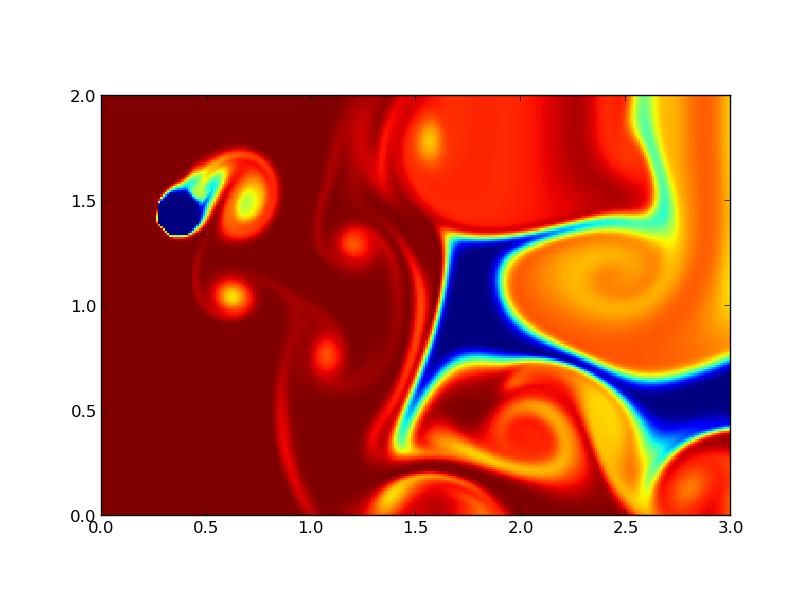
FIG 8 - Obstacle oscillant verticalement
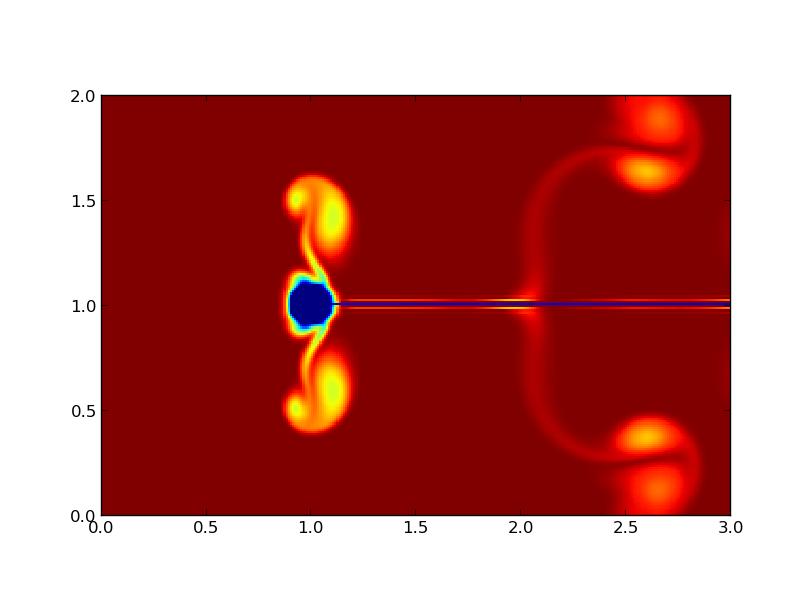
FIG 9 - Obstacle oscillant horizontalement
3.3 Propulsion
On peut aussi utiliser un obstacle mobile plus complexe, sous la forme d'un segment qui bat dans le fluide. Pour éviter de devoir modéliser un rectangle oscillant sous python, nous avons simplement empilé des obstacles sphériques identiques à ceux de la section 3.2. On évite ainsi la rotation puisque chaque sphère n'est qu'en translation.
Nous avions, tout d'abord, utilisé des obstacles sphériques oscillants verticalement (figure 10) mais cela ne correspondait pas à la réalité physique d'un objet en mouvement parce que la longueur de l'obstacle composé change au cours du battement et la vitesse n'a qu'une composante verticale. Nous les avons donc remplacés par des obstacles sphériques en mouvement sur un arc de cercle, de telle sorte que l'on reproduit bien la rotation de l'obstacle composé. Les résultats (figure 11) sont légèrement différents mais le comportement général reste le même : on a aussi des allées de Von Kármán mais elles sont bien plus étirées verticalement et bien plus chaotiques.
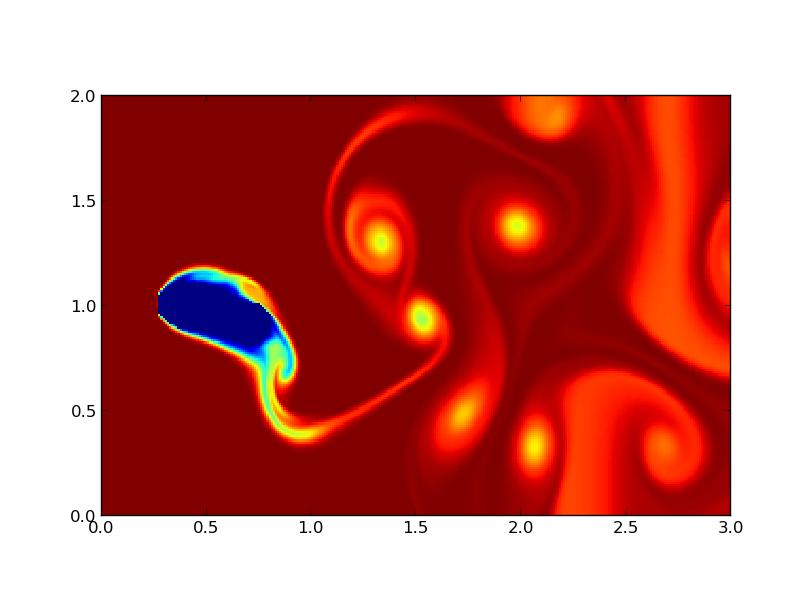
FIG 10 - Propulsion avec oscillations
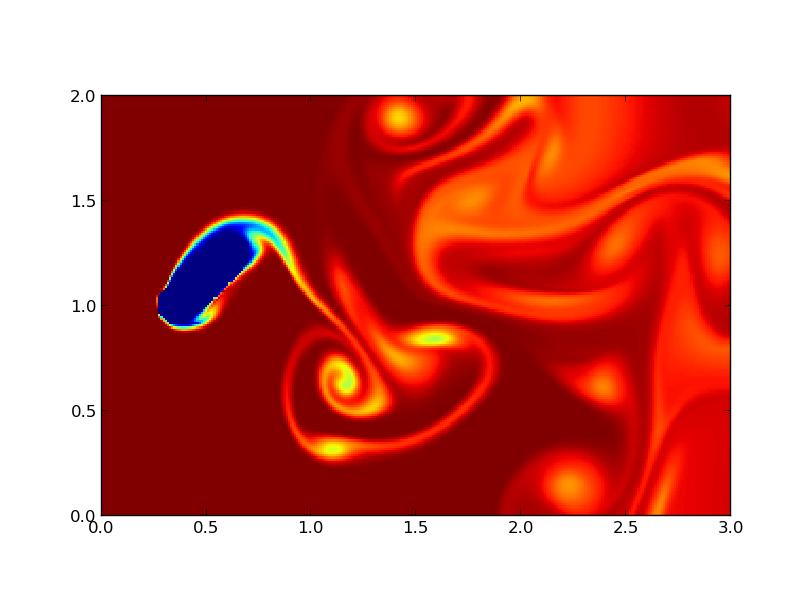
FIG 11 - Propulsion avec un mouvement circulaire
4 Différents résultats sans écoulement global U=0
On peut enfin utiliser notre programme pour observer d'autres phénomènes physiques que les allées de Von Kármán. Nous avons ainsi utilisé les mêmes obstacles mobiles que dans la section 3 pour mettre en mouvement le fluide, sans vitesse initiale. Il suffit pour cela de lancer le programme sans imposer de vitesse et en laissant la pression libre sur la paroi de gauche pour que le fluide puisse circuler. On impose également un colorant de 1 sur toute la surface à l'état initial.
4.1 Obstacle oscillant
Nous avons ici utilisé les obstacles oscillants horizontalement et verticalement. Leur mouvement entraîne le fluide comme dans les figures 8 et 9. Sur la figure 12 on voit un obstacle oscillant verticalement avec des plaques sur les parois haute et basse. Lorsque le fluide en mouvement vertical les rencontre, il est donc dévié et se propage sur les cotés. On a la même chose sur la figure 13. Dans ce cas, les plaques n'entravent pas le mouvement du fluide.
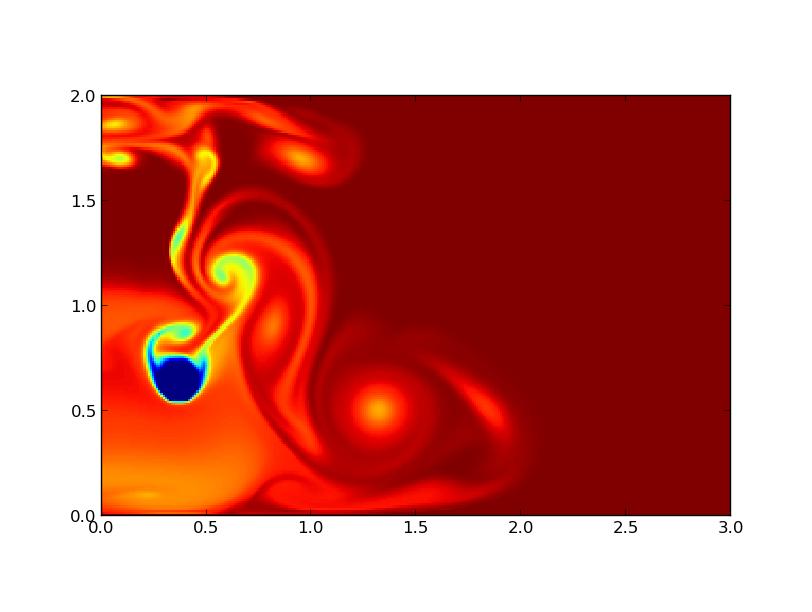
FIG 12 - Obstacle oscillant verticalement
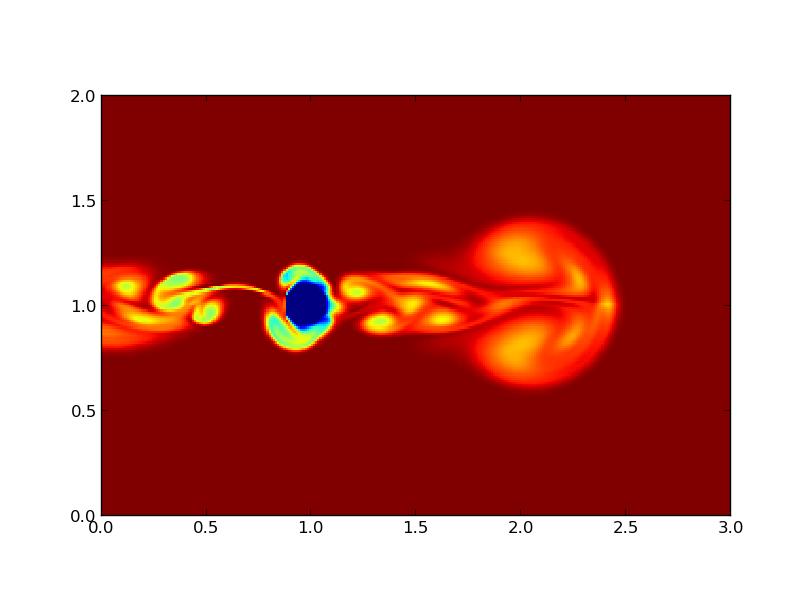
FIG 13 - Obstacle oscillant horizontalement
4.2 Propulsion
Nous avons enfin utilisé les obstacles composés de la section 3.3 pour propulser de l'eau immobile au départ, comme le ferait un éventail. Si on laisse des conditions aux limites libres sur les parois haute et basse, le fluide sera brassé par l'obstacle mais sans progresser dans une direction précise. On le confine donc entre deux plaques, mais la configuration utilisée dans la section 3 n'est pas très efficace car l'obstacle reste loin des plaques Nous l'avons donc rallongé pour obtenir une propulsion.
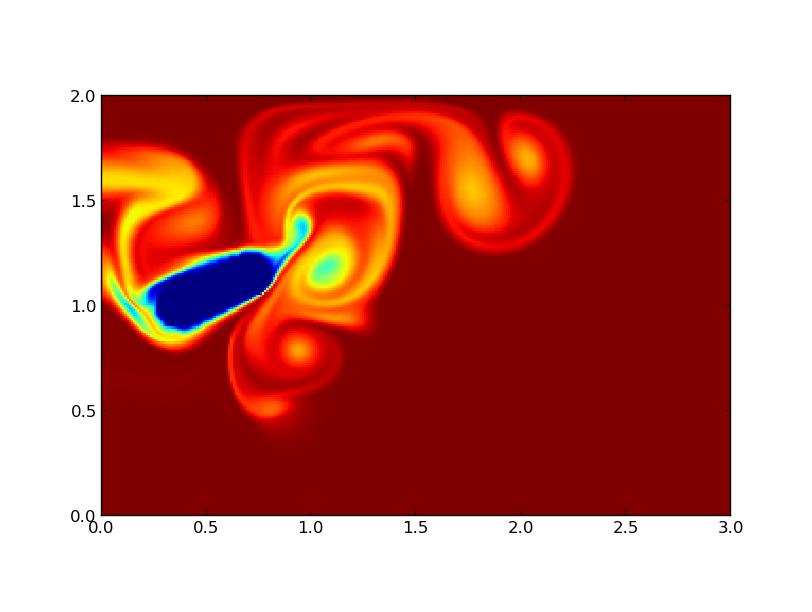
FIG 14 - Propulsion avec oscillations
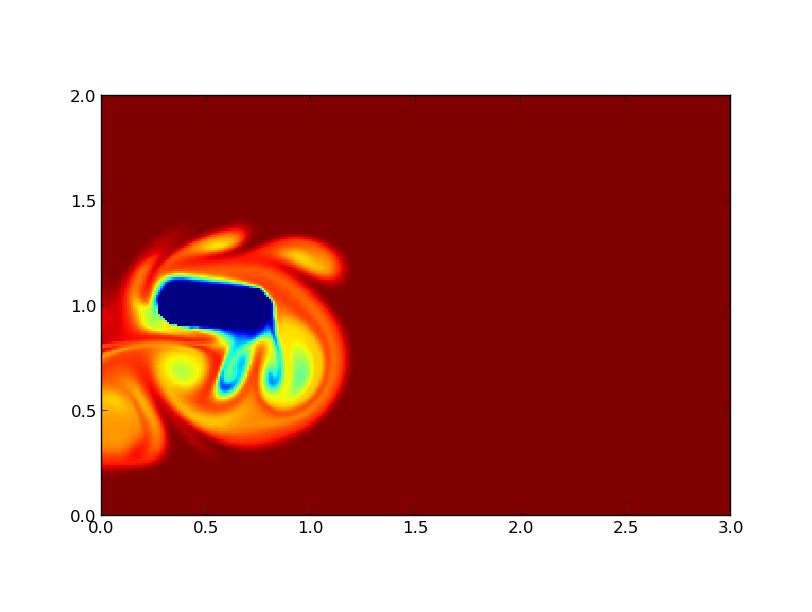
FIG 15 - Propulsion avec un mouvement circulaire
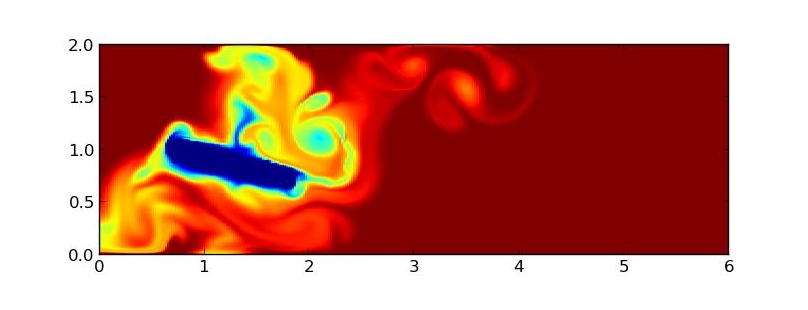
FIG 16 - Propulsion avec un mouvement circulaire