Travail d'Initiative Personnelle Encadré : Théorie du Chaos (Janvier-Juin 2012)
L'épreuve du TIPE est une composante des concours d'entrée aux grandes écoles. Lors de l'année 2011-1012, le thème obligatoire était 'Prévision'. J'ai donc décidé d'étudier certains systèmes chaotiques (dans le cadre de la prévisibilité du mouvement des systèmes physiques) et certaines de leurs propriétés via des études théoriques, numériques et expérimentales dans des domaines variés de la physique au programme des classes préparatoires PC : le pendule forcé en mécanique, l'oscillateur de Chua en électrocinétique et la convection de Rayleigh-Bénard en hydrodynamique.
TIPE réalisé au Lycée René Cassin de Bayonne pendant l'année scolaire 2011-2012.
Problématique : Peut-on prévoir précisément l'évolution d'un système dans le temps ?
Sommaire
Introduction
La prévision de multiples systèmes est nécessaire ou tout simplement voulue dans la vie contemporaine. Par exemple, l’évolution d’un système électrique doit être connue très précisément dans le cadre des machines électroniques (informatique, appareils ménagers, ...) pour éviter les dysfonctionnements pouvant être dangereux. De même, dans d'autres domaines tels que l'économie, la météorologie et la biologie, la prévision a un rôle très important et utile de nos jours. Or, dans ces domaines la prévision est difficile vu que les systèmes étudiés peuvent être chaotiques. C’est pour cela que j’ai, tout d'abord, montré l'existence de ces systèmes chaotiques en physique avec l'exemple du pendule forcé puis, dans un second temps, j'ai étudié l’oscillateur de Chua ,d’une part, et la convection de Rayleigh−Bénard décrivant les mouvements convectifs de l’atmosphère ou du manteau terrestre, d’autre part, pour montrer l'existence du chaos en électricité et en météorologie. Les divers systèmes (pendule forcé, oscillateur de Chua et convection de Rayleigh−Bénard) ont été étudiés de la manière suivante : tout d'abord, l'établissement des équations − non linéaires − du mouvement à l’aide des théorèmes classiques de mécanique ou d’électronique, puis à l’aide du logiciel informatique Maple, une visualisation des solutions de ces équations. Enfin, ces systèmes ont été étudiés de façon expérimentale pour corroborer, du mieux possible, les résultats théoriques en visualisant ces solutions et en obtenant l'attracteur étrange expérimental.
1 Mise en évidence des systèmes chaotiques
1.1 Étude du pendule libre
Mise en équation
Système : {masse M + tige rigide de masse m ≪ M}
Référentiel : terrestre supposé galiléen (noté Rt)
Coordonnées : cylindriques $(O,\vec{e_r},\vec{e_\theta},\vec{e_z})$
On observe un mouvement de rotation autour de l'axe $\Delta=(O,\vec{e_z})$ et d'angle θ.
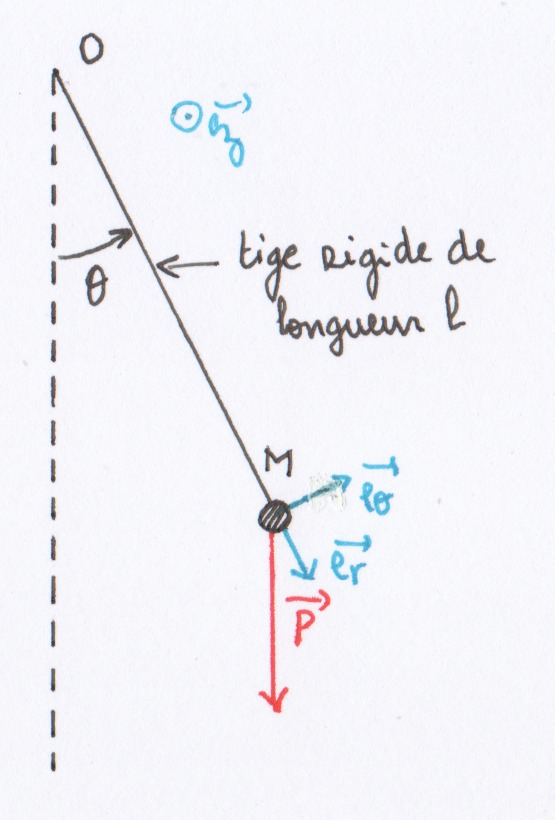
FIG 1 - Schéma du pendule libre
Théorème du moment cinétique par rapport à l'axe Δ=(O,$\vec e_z$) $$\frac{d \sigma_\Delta}{dt}= \sum_i M_\Delta(\vec F_i)$$
Moment cinétique $$\sigma_\Delta=\vec \sigma_O . \vec e_z = M l^2 \dot \theta $$
Forces extérieures
- Poids $\vec P= m \vec g = m(\cos \theta \vec e_r - \sin \theta \vec e_\theta)$ de moment $M_\Delta(\vec P) = (\vec{OM}\wedge\vec P).\vec e_z = - mgl \sin \theta$
- Liaison pivot en O supposée parfaite
- Frottements fluides négligés
Equation du mouvement $$\ddot \theta + \frac{g}{l} \sin \theta =0$$
Cas de petites oscillations
On considère des mouvements de faible amplitude : sin θ ∼ θ, pour cela il faut avoir θ < 16°.
On obtient alors le système de Cauchy : $$\ddot \theta (t) + \frac{g}{l} \theta (t) =0$$ $$\theta(0)=\theta_0$$ $$\dot \theta (0) = \dot \theta_0 $$
Solution du système
$$\theta (t)= \theta_0 \cos(\omega t) + \frac{\dot \theta_0}{\omega_0} \sin(\omega_0 t) \text{ avec } \omega_0^2=\frac{g}{l}$$
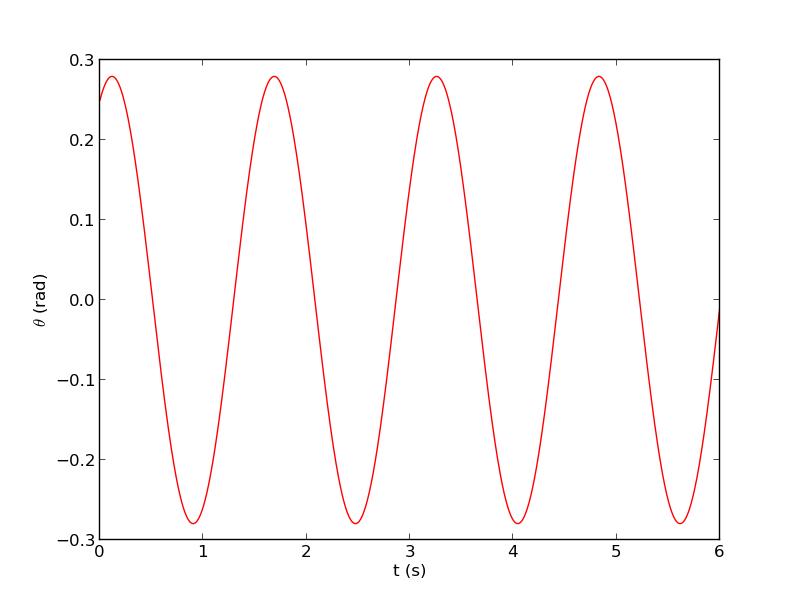
FIG 2 - Courbe de θ(t) pour θ0=0.25 rad, $\dot \theta_0$=0.5 rad/s, ω0=4 rad/s
Pour deux conditions initiales proches $\theta_1(0)=\theta_2(0)+\delta \theta_0$ avec $\delta \theta_0 \ll (\theta_1(0),\theta_2(0))$ et $\dot \theta_1(0)=\dot \theta_2(0)+\delta \dot \theta_0$ avec $\delta \dot \theta_0 \ll (\dot \theta_1(0),\dot \theta_2(0))$. Soit $\Delta \theta (t)= \theta_1(t)-\theta_2(t)$, on obtient $$\Delta \theta (t)= \delta \theta_0 \cos(\omega t)+ \frac{\delta \dot \theta_0}{\omega_0} \sin(\omega_0 t) \text{ avec } \omega_0^2=\frac{g}{l}$$ Comme $|\cos(\omega_0 t)| \le 1$ et $|\sin(\omega_0 t)| \le 1$, on a alors $$\Delta \theta(t) \ll (\theta_1(t),\theta_2(t))$$ On peut donc prévoir l'évolution du système au cours du temps. On dit alors que le système est NON CHAOTIQUE.
1.2 Étude du pendule forcé
Mise en équation
Système : {masse M + tige rigide de masse m ≪ M}
Référentiel : terrestre supposé galiléen (noté Rt)
Coordonnées : cylindriques $(O,\vec{e_r},\vec{e_\theta},\vec{e_z})$
On observe un mouvement de rotation autour de l'axe $\Delta=(O,\vec{e_z})$ et d'angle θ. La vitesse de la masse M est donnée par $\vec v = l \dot \theta \vec{e_\theta}$ dans le référentiel terrestre. D'où la vitesse de l'écoulement de l'air au voisinage de la masse est $\vec v = - l \dot \theta \vec{e_\theta}$ dans le référentiel lié à la masse. Soit Re le nombre de Reynolds de cet écoulement : $Re= \frac{R v}{\nu}=\frac{R l \dot \theta}{\nu}$ avec ν la viscosité cinématique de l'air et R le rayon de la masse M.
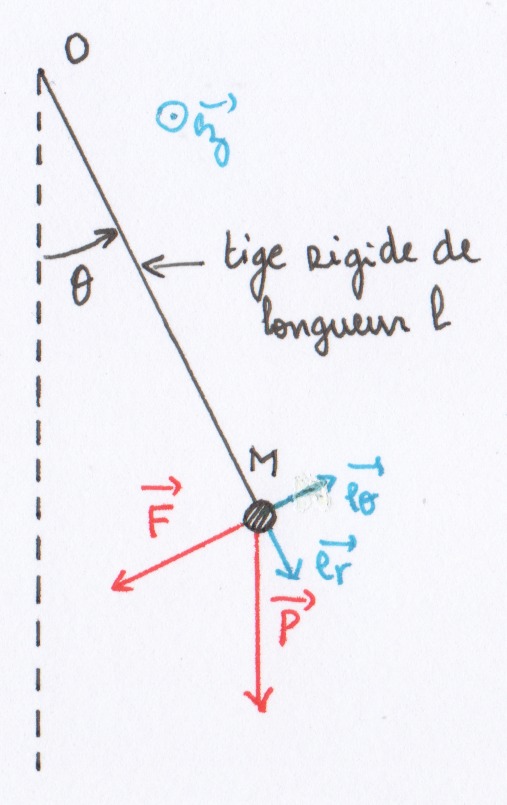
FIG 3 - Schéma du pendule amorti
Théorème du moment cinétique par rapport à l'axe $\Delta = (O,\vec e_z)$ $$\frac{d \sigma_\Delta}{dt}= \sum_i M_\Delta(\vec F_i) + \sum_i \vec C_i . \vec e_z$$
Moment cinétique} $$\sigma_\Delta=\vec \sigma_O . \vec e_z = M l^2 \dot \theta $$
Forces extérieures}
- Poids $\vec P= M \vec g = M(\cos \theta \vec e_r - \sin \theta \vec e_\theta)$ de moment $M_\Delta(\vec P) = (\vec{OM}\wedge\vec P).\vec e_z = - Mgl \sin \theta$
- Liaison pivot en O supposée parfaite
- Frottements fluides sur la masse (négligés sur la tige) :
- si $Re \ll 1$, $\vec F=-k \vec v$ avec $k>0$ de moment $M_\Delta(\vec F) = (\vec{OM}\wedge\vec F).\vec e_z = - kl^2 \dot \theta$
- si $Re > 1000$, $\vec F=-k' v \vec v$ avec $k'>0$ de moment $M_\Delta(\vec F) = (\vec{OM}\wedge\vec F).\vec e_z = - k' l^3 \dot \theta^2$
- Couple moteur exercé en O : $\vec C = \alpha \sin(\omega t) \vec e_z$
Equation du mouvement$$\ddot \theta + \frac{k}{M} \dot \theta + \frac{g}{l} \sin \theta = \frac{\alpha}{Ml^2}\sin(\omega t) \text{ si } Re \ll 1$$ $$\ddot \theta + \frac{k' l}{M} \dot \theta^2 + \frac{g}{l} \sin \theta = \frac{\alpha}{Ml^2}\sin(\omega t) \text{ si } Re > 1000$$
Cas d'un mouvement dans un écoulement visqueux Re ≪ 1
On a l'équation $\ddot \theta + \frac{\omega_0}{Q} \dot \theta + \omega_0^2 \sin \theta = \rho \sin(\omega t)$ avec $\omega_0=\sqrt{\frac{g}{l}}$, $Q=\frac{M\omega_0}{k}$ et $\rho = \frac{\alpha}{Ml^2}$ d'après l'équation \eqref{PF1}.
Pour deux conditions initiales proches θ1(0)=θ2(0)+δθ0 avec δθ0 ≪ (θ1(0),θ2(0)) et $\dot \theta_1$(0)=$\dot \theta_2$(0)+$\delta \dot \theta_0$ avec $\delta \dot \theta_0$ ≪ ($\dot \theta_1$(0),$\dot \theta_2$(0))
D'après la loi de Stokes, $k=6 \pi \eta R$ avec R le rayon de la masse M et $\eta$ la viscosité dynamique de l'écoulement de l'air.
On utilise une résolution numérique avec MAPLE (méthode Runge Kutta à l'ordre 4). $\eta=3.10^{-5} Pl$, $R=2 cm$, $M=1 kg$, $l=1 m$, $\rho=10 s^{-2}$, $\omega=1 rad/s$ ainsi que $\theta_1(0)=30°$, $\theta_2(0)=30,1°$.

FIG 4 - Courbes temporelles de θ
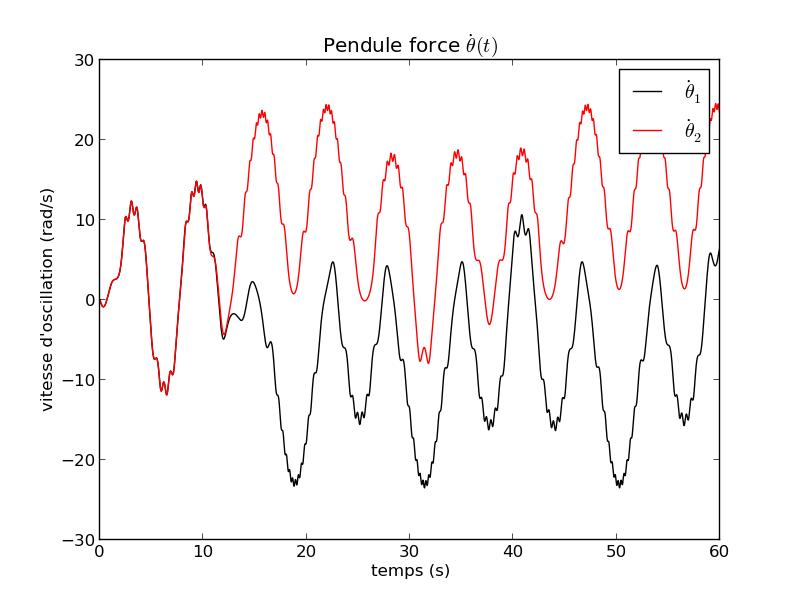
FIG 5 - Courbes temporelles de $\dot \theta$ pour Q=3,1.10-5, ω0=3,1 rad/s et ρ=10 s-2
Pour t>t0=10s : Δθ(t)=θ1(t)-θ2(t) n'est plus négligeable devant θ1(t) et θ2(t). Donc on ne peut pas savoir quel sera l'angle à cet instant : cela pourra être θ1(t), θ2(t) ou un angle entre les deux, vu qu'une précision plus petite sur les conditions initiales (3/1000) ne pourra pas être réalisée.
On ne peut donc pas prévoir l'évolution du système pour un temps grand devant t0. On dit alors que le système est CHAOTIQUE.
Allure de la vitesse : On obtient $|\dot \theta (t)|$ < 25 rad/s. Donc Remax=2,5.104>1000 : à la vitesse maximale de la masse, l'écoulement est turbulent donc $\vec F=-k' v \vec v$ et non pas $\vec F=-k \vec v$: le modèle pris en compte ne tient pas compte de la réalité.
Paramètre de contrôle ρ : Il existe un réel positif $\rho_0$ tel que si $\rho$ < $\rho_0$ alors le système est prévisible (non chaotique). $\rho_0$ dépend des valeurs de $\omega_0$, Q, $\omega$ ainsi que des conditions initiales. Dans ce cas, le système évolue vers un attracteur périodique fixé par le moteur. $\rho$ est appelé paramètre de contrôle du chaos.
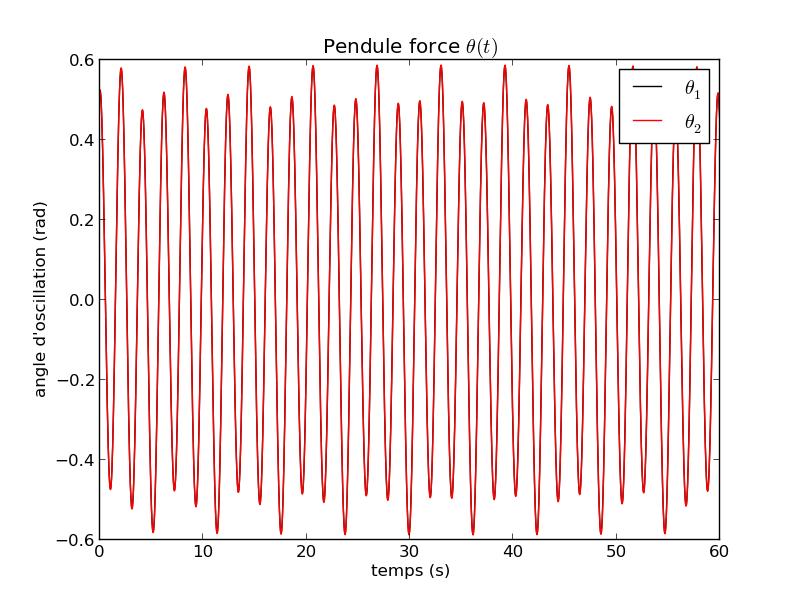
FIG 6 - Courbe temporelle de θ pour ρ=0.5
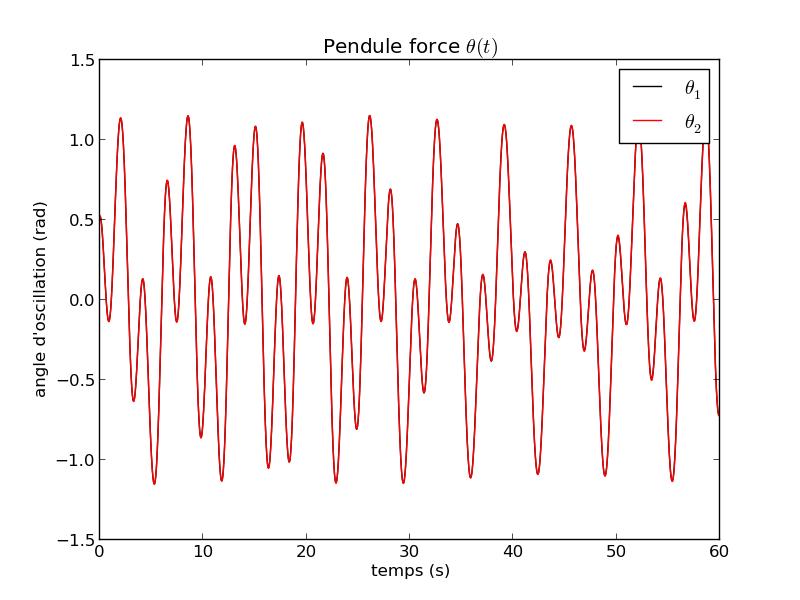
FIG 7 - Courbe temporelle de θ pour ρ=4.5
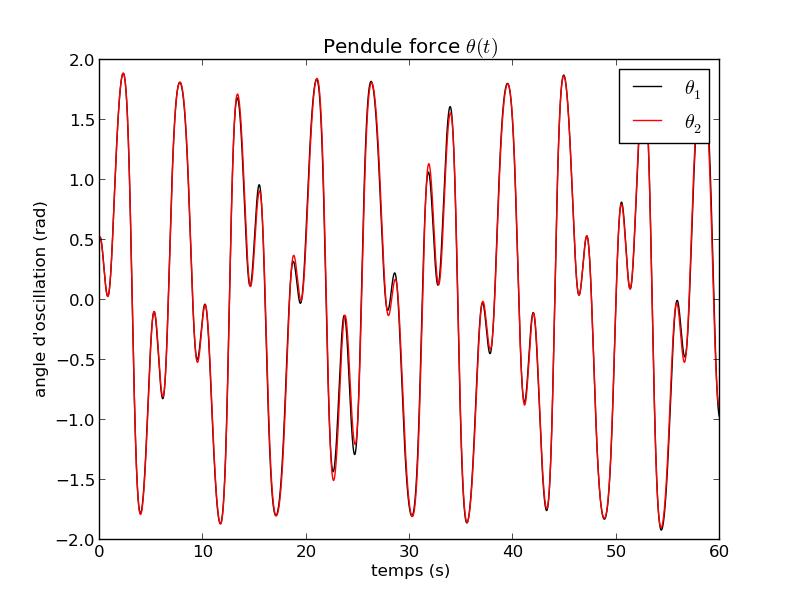
FIG 8 - Courbe temporelle de θ pour ρ=7.2
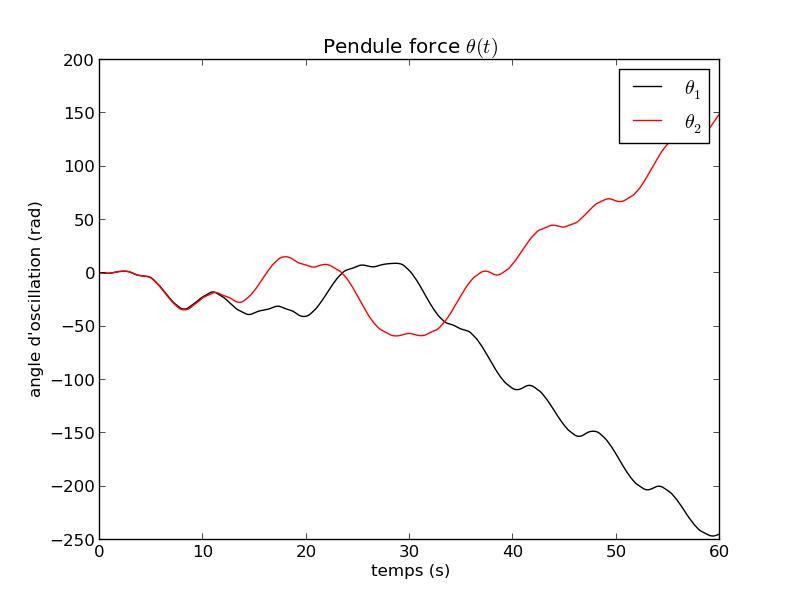
FIG 9 - Courbe temporelle de θ pour ρ=7.4
D'où ici ρ0 est de l'ordre de 7.5 s-2. Il est obtenu de façon empirique.
Cas d'un mouvement dans un écoulement turbulent
On a l'équation $\ddot \theta + K \dot \theta^2 + \omega_0^2 \sin \theta = \rho \sin(\omega t)$ avec $\omega_0=\sqrt{\frac{g}{l}}$, $K=\frac{k' l}{M}$ et $\rho = \frac{\alpha}{Ml^2}$ d'après l'équation \eqref{PF2}.
Pour deux conditions initiales proches $\theta_1(0)=\theta_2(0)+\delta \theta_0$ avec $\delta \theta_0 \ll (\theta_1(0),\theta_2(0))$ et $\dot \theta_1(0)=\dot \theta_2(0)+\delta \dot \theta_0$ avec $\delta \dot \theta_0 \ll (\dot \theta_1(0),\dot \theta_2(0))$
Pour un écoulement turbulent, $k'=\frac{1}{2} C \mu \pi R^2$ avec R le rayon de la masse M et $\mu$ la masse volumique de l'air et C le coefficient de trainée (C=0.4 pour une sphère).
On utilise une résolution numérique avec MAPLE (méthode Runge Kutta à l'ordre 4). $\mu=1.3 kg/m^3$, $R=2 cm$, $M=1 kg$, $l=1 m$, $\rho=10 s^{-2}$, $\omega=1 rad/s$ ainsi que $\theta_1(0)=30°$, $\theta_2(0)=30,1°$
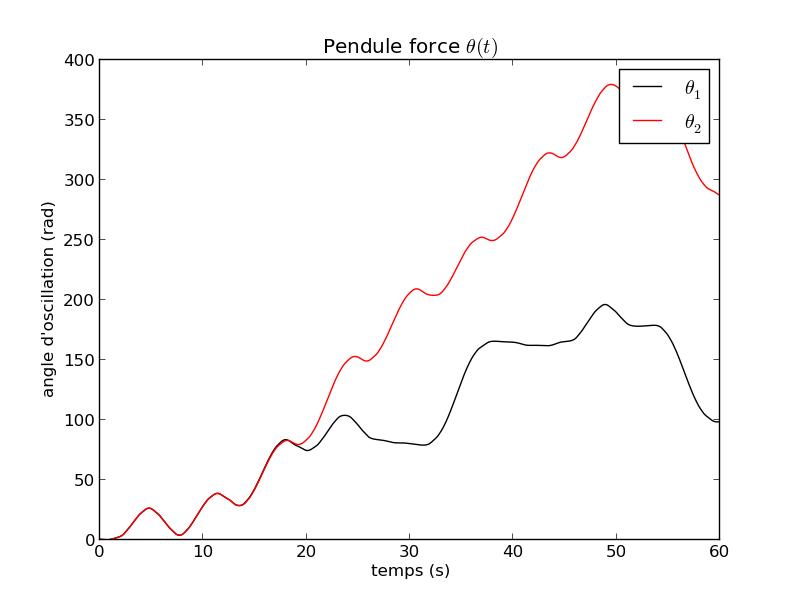
FIG 10 - Courbe temporelle de θ
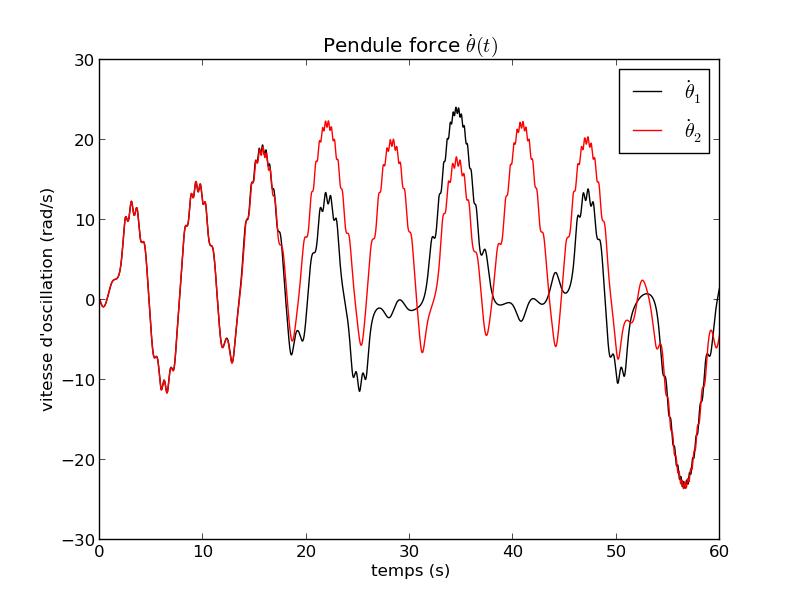
FIG 11 - Courbe temporelle de $\dot \theta$ pour K=3,2.10-4, ω0=3,1 rad/s et ρ=10 s-2
Pour $t>t_0=18s$ : $\Delta \theta (t)= \theta_1(t)-\theta_2(t)$ n'est plus négligeable devant $\theta_1(t)$ et $\theta_2(t)$.
On ne peut donc pas prévoir l'évolution du système pour un temps grand devant $t_0$. \\ On dit alors que le système est CHAOTIQUE.
Allure de la vitesse : On obtient $|\dot \theta (t)| < 25 rad/s$. Donc $Re_{max}= 2.5 ~10^4 >1000 $: à la vitesse maximale de la masse, l'écoulement est turbulent donc on a bien $\vec F=-k' v \vec v$. Le modèle semble donc correct pour les valeurs prises pour l'étude.
Donc le système pendule forcé est bien chaotique.
Paramètre de contrôle ρ : De même que précédemment, ρ est un paramètre de contrôle du chaos.
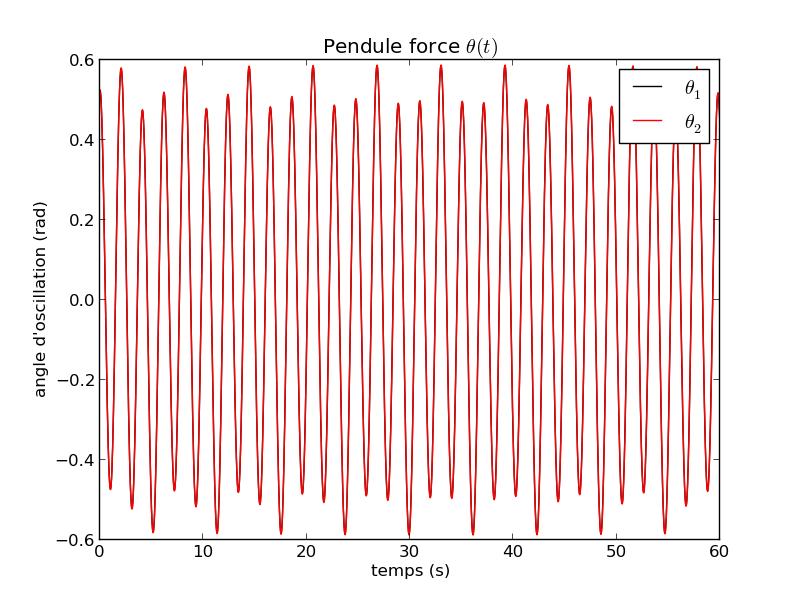
FIG 12 - Courbe temporelle de θ pour ρ=0.5
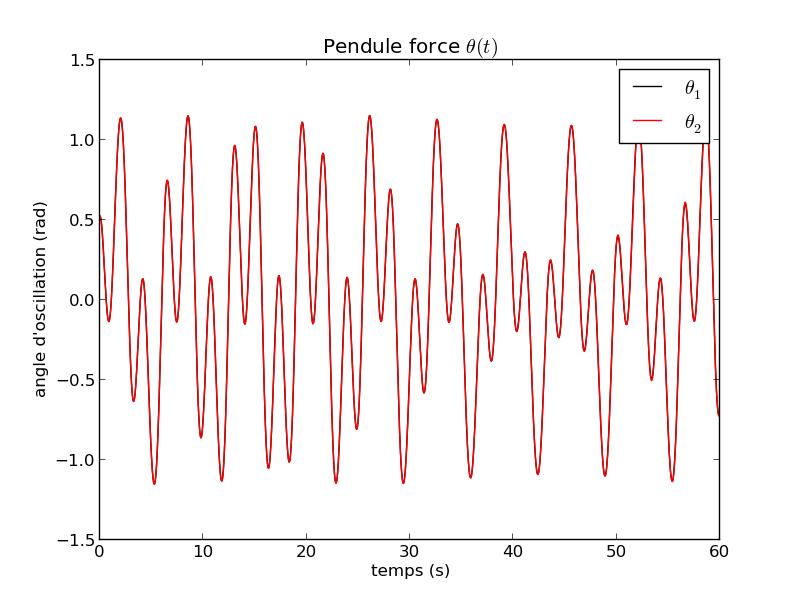
FIG 13 - Courbe temporelle de θ pour ρ=4.5
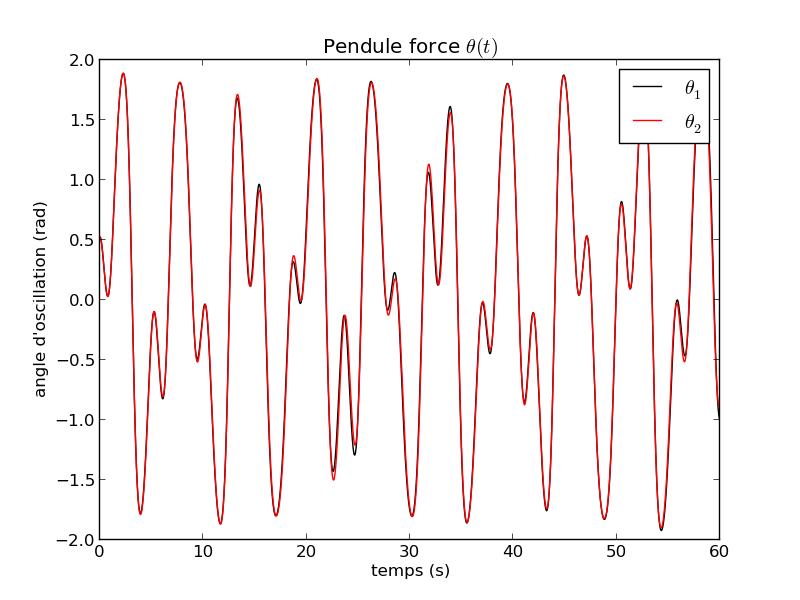
FIG 14 - Courbe temporelle de θ pour ρ=7.2
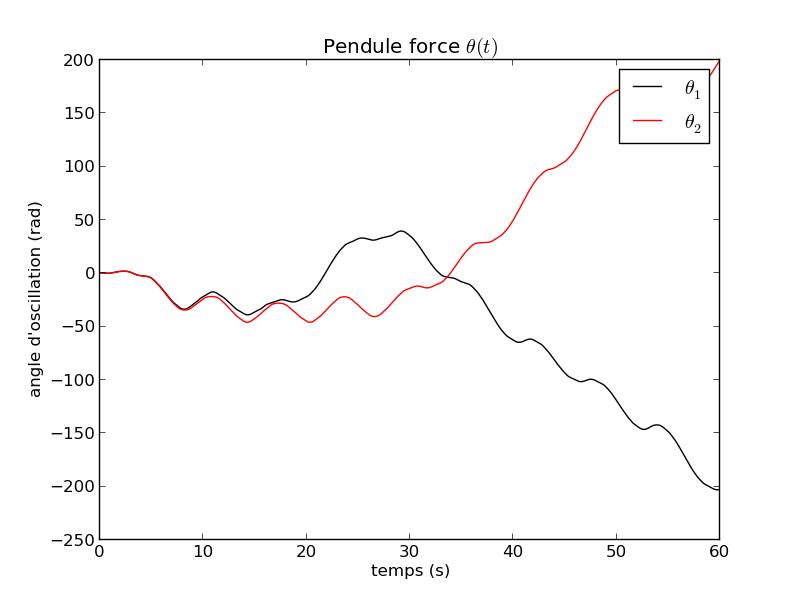
FIG 15 - Courbe temporelle de θ pour ρ=7.4
On obtient également ρ0=7.5 s-2.
Résultats expérimentaux
Montage : On force un pendule pesant à l'aide d'un autre pendule et d'un générateur de tension continue.
FIG 16 - Montage
Mesures temporelles : On observe cette même courbe pour cinq relevés différents :
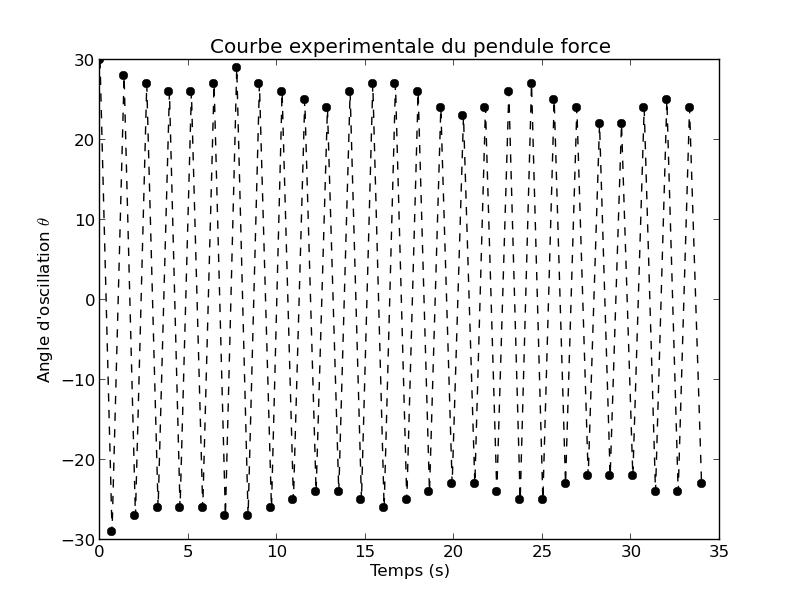
FIG 17 - Courbe obtenue
Période : 0.68 secondes
Le système est donc non chaotique (on se trouve dans le cas où $\rho < \rho_0$). Pour qu'il soit chaotique, il aurait fallu avoir un pendule forcé qui puisse faire des tours complets (impossible ici).
1.3 Systèmes déterministes et chaos
Repères historiques
Antiquité En 400 avant Jésus Christ, Pythagore définit le chaos comme « ce qui ne peut s'exprimer sous forme mathématique ».
XVIe – XVIIe siècle De grands scientifiques comme Galilée, Copernic, Kepler, Newton s'intéressent à la mécanique céleste et trouvent des lois régissant le monde. C'est le début de la mécanique déterministe. Kepler trouve trois lois (qui portent son nom) démontrées par Newton à l'aide de la découverte de la force de gravitation en $\frac{1}{r^2}$ et des lois portant son nom, établissant les lois fondamentales de la mécanique classique. Newton établit alors des principes déterministes :
- Les mêmes causes produisent les mêmes effets.
- Un système simple possède un comportement simple.
- Une augmentation de la précision des mesures donne de meilleurs résultats.
XIXe siècle Laplace établit en 1814 que le problème à 3 corps célestes est non chaotique avec une approximation des résultats à l'ordre 1 et établit que « tout phénomène physique est prévisible si l'on connaît ses causes ». C'est une période où le déterminisme est triomphant. Cependant, certaines contradictions apparaissent. Maxwell montre que des imprécisions sur les conditions initiales peuvent faire varier les résultats et montre également la possibilité de l'irréversibilité en thermodynamique. Cela contredit le premier principe de Newton. De plus, Poincaré reprend en 1887 le problème à n corps en mécanique céleste. Il montre que le hasard est présent dans l'univers et démontre en plus la sensibilité aux conditions initiales de certains systèmes tels que le système solaire, qui s'avère à l'inverse de la conclusion de Laplace, chaotique. En 1892, Lyapounov mesure la divergence entre deux orbites issues de conditions initiales voisines. Il découvre une croissance exponentielle de caractéristique $\tau$ : l'horizon de Lyaponov.
XXe siècle Le début du XXe siècle assiste à trois révolutions en physique : la relativité d'Einstein en 1905, la mécanique quantique avec le principe d'Heisenberg en 1926 et le chaos avec Lorenz en 1963, initié par Poincaré en 1887. Dans les années 60-70, le chaos s'impose devant la scène scientifique avec les progrès informatiques permettant la visualisation des résultats mathématiques complexes. Le terme de chaos est alors introduit par Tien-Yien Li et James A. Yorke. En 1960, Faugenbaum montre les dédoublements de période suivant les caractéristiques du système et donc le contrôle possible de chaos. En 1963, Lorenz découvre le chaos en météorologie, problème qu'il simplifie à l'aide du modèle de la convection de Rayleigh-Bénard plus facile à résoudre grâce à seulement 3 degrés de liberté. Il met en avant la sensibilité aux conditions initiales qu'il redécouvre avec ses résultats malgré ses approximations. Il introduit alors l'effet papillon.
Règles et définitions du chaos
Un système est CHAOTIQUE si on ne peut pas prévoir son évolution à long terme tout en étant déterministe.
Causes Le chaos est dû à la sensibilité aux conditions initiales, causée par des phénomènes non linéaires et la forte récurrence du système.
Evolution de l'imprécision au cours du temps $$\Delta x(t)=\Delta x(0)e^{\lambda t}$$ λ est appelé exposant de Lyapunov : il dépend du système étudié et des conditions initiales. Si λ < 0 alors le système n'est pas chaotique. Si λ > 0 alors le système est chaotique et imprévisible pour $t \gg \frac{1}{\lambda}$. La valeur de Δ x(0) n'est jamais nulle car la valeur de la condition initiale n'est jamais indéfiniment précise lors d'une expérience.
Contrôle du chaos Comme nous l'avons vu dans le cas du pendule forcé, le chaos peut être contrôler grâce à un paramètre (ρ dans l'exemple) qui selon sa valeur donnera des attracteurs différents au système à l'équilibre (ou pseudo-équilibre si le système est chaotique). Le phénomène chaotique peut bien être contrôler comme le montre le contrôle de la fission nucléaire (chaotique) dans les centrales à l'aide de barre de bore qui captent les neutrons créés par la fission.
Attracteur étrange Les phénomènes chaotiques convergent vers un attracteur dit étrange dans l'espace des phases. Il s'agit d'une suite infinie de points à dimension fractale, c'est-à-dire que sa courbe représentative a une longueur infinie dans un espace fini. Il est apériodique (la trajectoire de la courbe dans l'espace des phases ne passe qu'une fois par le même point). Deux trajectoires proches (avec un écart relatif inférieur à 1%) s'éloignent localement de façon exponentielle. On peut prévoir que le système passera par un certain état $(z,\dot z)$ dans l'espace des phases : il s'agit du côté prévisible des systèmes chaotiques. Chaque système chaotique dissipatif possède un attracteur étrange.
Exemples d’attracteurs étranges Attracteur étrange de Hénon : Il s'agit de l'attracteur étrange des orbites stellaires.Attracteur étrange de Pickover : Il s'agit d'une modélisation 3D d'une solution mathématique.Attracteur étrange de Gumowski-Mira : Il s'agit de l'attracteur étrange de particules se déplaçant à hautes vitesses dans un accélérateur de particules de forme cylindrique.On remarque bien que le système chaotique se démarque des autres systèmes déterministes qui forment dans l'espace des phases une ellipse (système oscillant non amorti), une spirale convergeant vers l'origine (système oscillant dissipatif) ou divergente (système oscillant amplificateur), ...
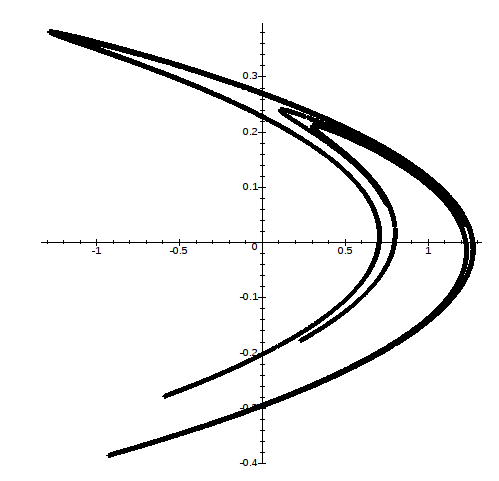
FIG 18 - Attracteur de Henon
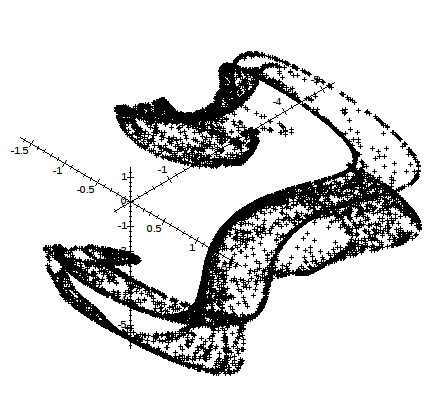
FIG 19 - Attracteur de Pickover
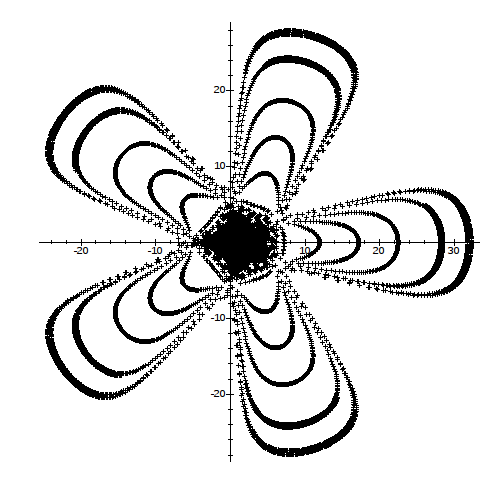
FIG 20 - Attracteur de Gumovski-Mira3
2 Application à l'oscillateur de Chua
2.1 Position du problème
Oscillateur de Chua
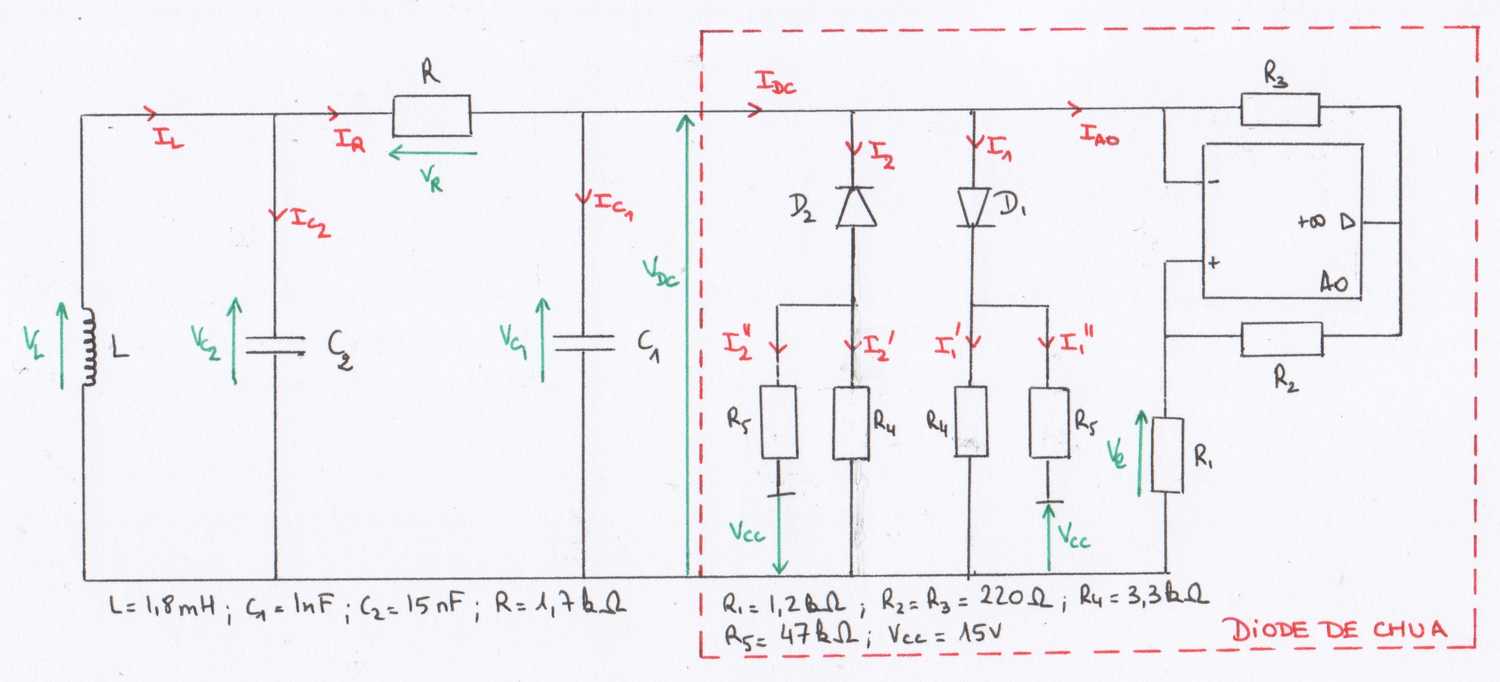
FIG 21 - Schéma de l'oscillateur de Chua
Approximations
- On considérera l'amplificateur opérationnel idéal, on ne tiendra pas compte de son comportement fréquentiel.
- On considérera la diode comme idéale (cf sa caractéristique ci-dessous).
- On négligera la résistance de la bobine (quelques ohms) et celle des fils.
2.2 Mise en équation
Caractéristique de la diode de Chua
Schéma de la diode de Chua
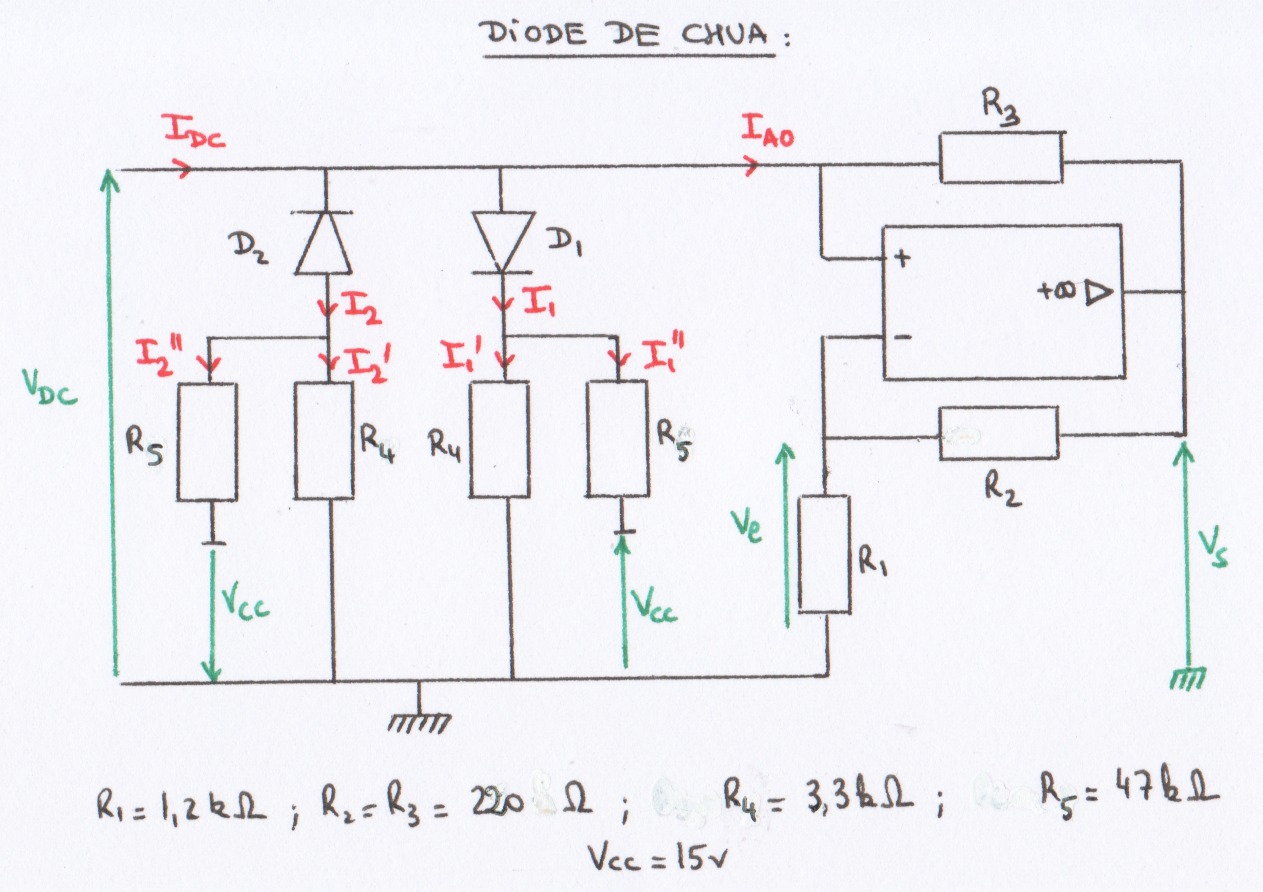
FIG 22 - Schéma de la diode de Chua
Partie amplificateur opérationnel : $I_{AO}=f(V_e)$.
La sortie de l'amplificateur opérationnel (AO) est rebouclée sur la borne inverseuse donc l'AO fonctionne en régime linéaire : on a alors $V^+=V^-=V_e$ $$V_e = \frac{R_1}{R_1+R_2} \text{ et }V_e - V_s = R_3 I_{AO}$$ Donc $$ V_e(1- \frac{R_1+R_2}{R_1})=R_3 I_{AO} \Rightarrow V_e=V_{DC}= -\frac{R_1 R_3}{R_2} I_{AO} = R' I_{AO}$$
Le circuit est équivalent à une résistance négative de valeur $R'=-\frac{R_1 R_3}{R_2}$
Caractérisque de la diode de Chua : $I_{DC}=f(V_{DC})$
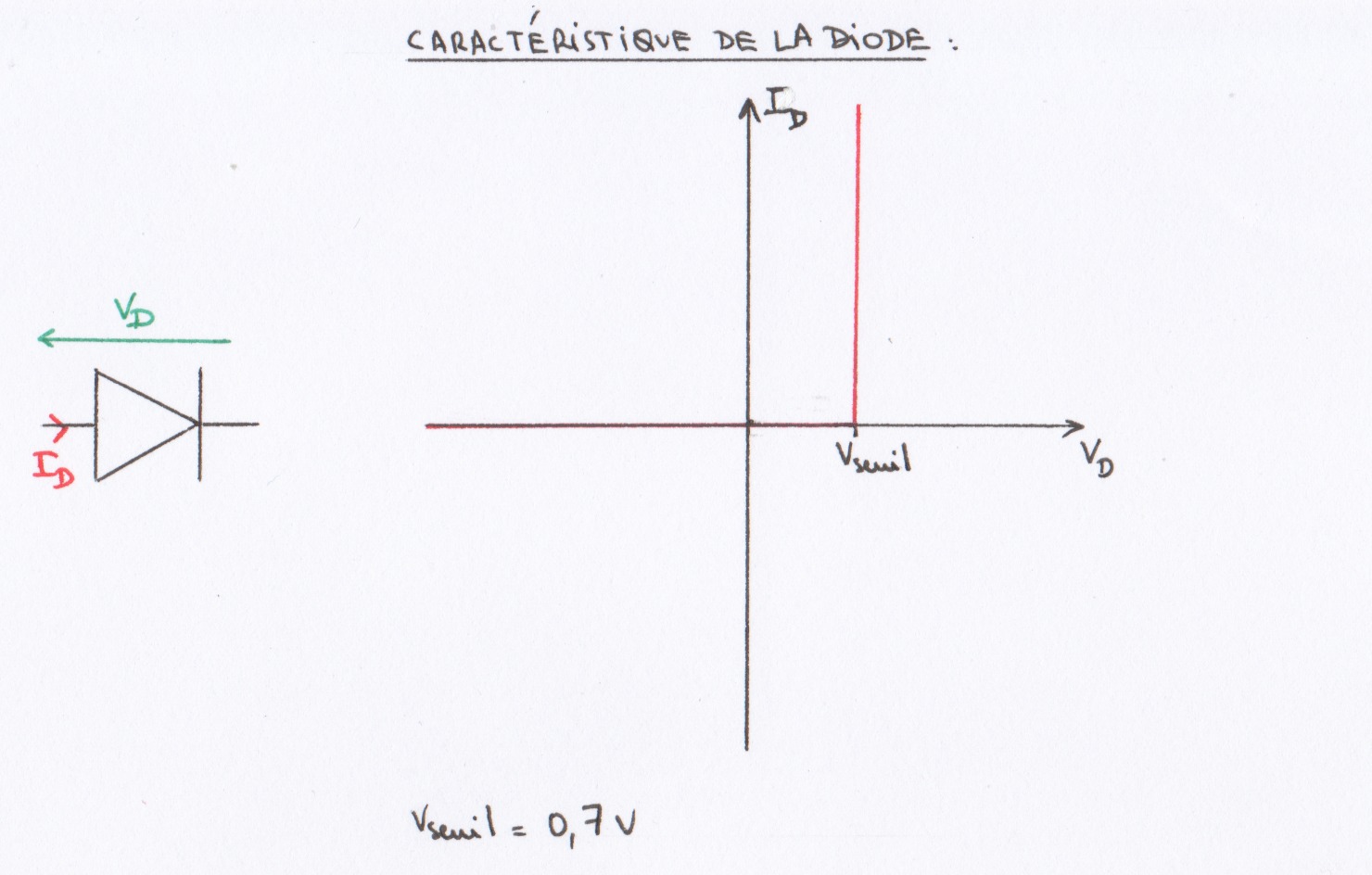
FIG 23 - Caractéristique de la diode Di
Soit $U_{R_i}$ la tension aux bornes de $R_i$ en convention récepteur.
Branche D1
$V_{D_1} < V_{seuil}$ : la diode $D_1$ est non passante d'où $U_{R_4}=V_{DC}-V_{D_1}=\frac{R_4}{R_4+R_5} V_{cc}$ $$V_{DC} ≤ V_{seuil} + \frac{R_4}{R_4+R_5} V_{cc} = U_c$$
Branche D2
$V_{D_2} < V_{seuil}$ : la diode $D_2$ est non passante d'où $U_{R_4}=V_{DC}+V_{D_2}=-\frac{R_4}{R_4+R_5} V_{cc}$ $$V_{DC}>-V_{seuil} - \frac{R_4}{R_4+R_5} V_{cc} = - U_c$$
Caractéristique
- Si $V_{DC}<-U_c$, la diode $D_2$ est passante et la diode $D_1$ est non passante : $$I_{DC}=I_{AO}+I_2'+I_2''=\frac{V_{DC}}{R'}+\frac{V_{DC}+V_{seuil}}{R_4} + \frac{V_{DC}+V_{seuil}+V_{cc}}{R_5}$$ $$\boxed{I_{DC}= (\frac{1}{R'}+ \frac{1}{R_4} + \frac{1}{R_5}) V_{DC} + (\frac{1}{R_4} + \frac{1}{R_5}) V_{seuil} +\frac{V_{cc}}{R_5} = (\frac{1}{R'}+ \frac{1}{R_4} + \frac{1}{R_5}) V_{DC} + (\frac{1}{R_4} + \frac{1}{R_5}) U_c}$$
- Si $-U_c<V_{DC}<U_c$, les diodes sont non passantes : $$\boxed{I_{DC}=\frac{V_{DC}}{R'}}$$
- Si $V_{DC}>U_c$, la diode $D_1$ est passante et la diode $D_2$ est non passante : $$I_{DC}=I_{AO}+I_1'+I_1''=\frac{V_{DC}}{R'}+\frac{V_{DC}-V_{seuil}}{R_4} + \frac{V_{DC}-V_{seuil}-V_{cc}}{R_5}$$ $$\boxed{I_{DC}= (\frac{1}{R'}+ \frac{1}{R_4} + \frac{1}{R_5}) V_{DC} - (\frac{1}{R_4} + \frac{1}{R_5}) V_{seuil} -\frac{V_{cc}}{R_5} = (\frac{1}{R'}+ \frac{1}{R_4} + \frac{1}{R_5}) V_{DC} - (\frac{1}{R_4} + \frac{1}{R_5}) U_c}$$
On obtient la caractéristique de la diode de Chua suivante :
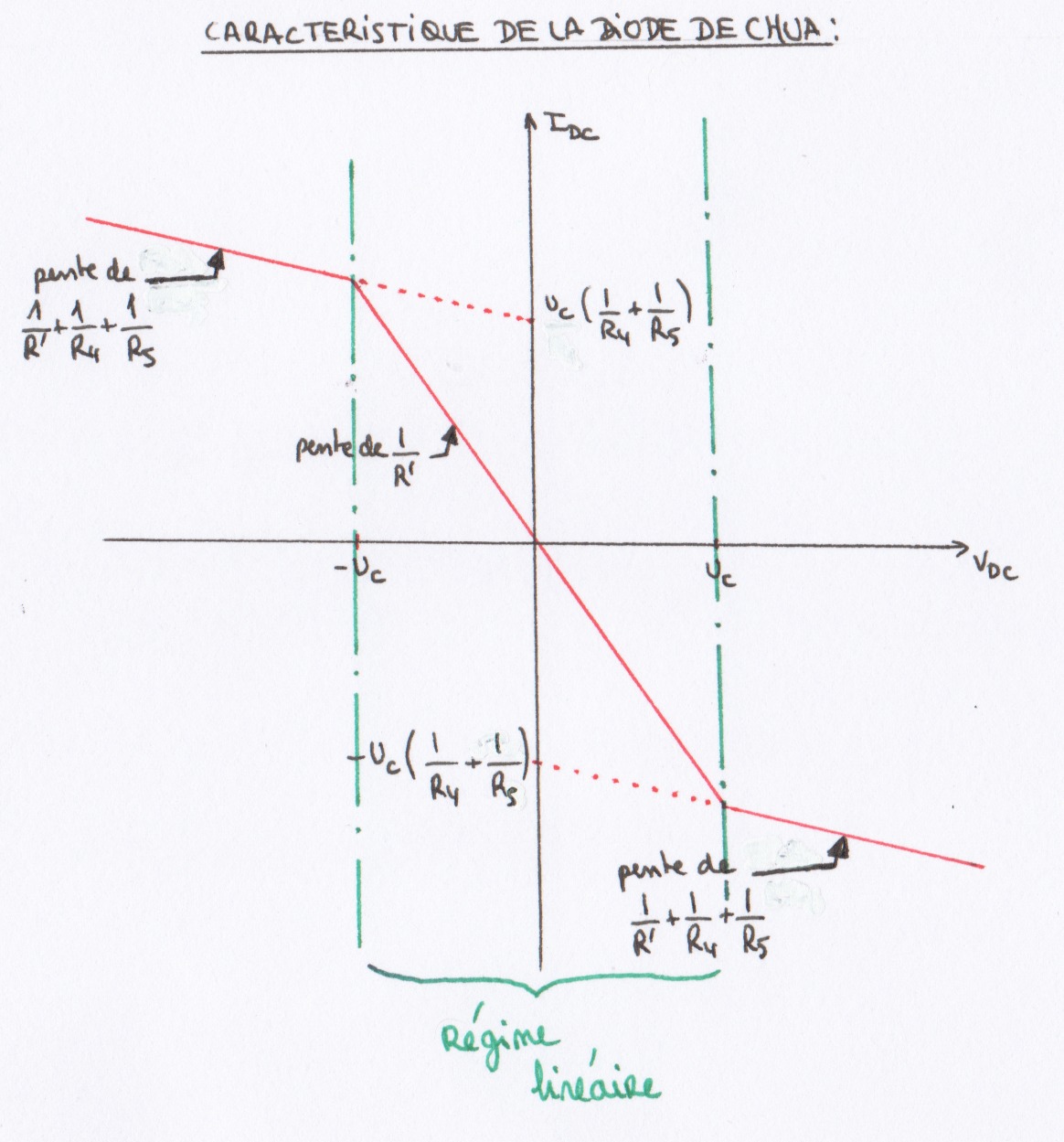
FIG 24 - Caractéristique de la diode de Chua
On vérifie bien que la caractéristique de la Diode de Chua est continue.
Pour les valeurs numériques citées ci-dessus, on a :
- Si $V_{DC} < -1.68v$, $I_{DC}= -5,1.10^{-4} V_{DC} + 5,5.10^{-4}$
- Si $-1.68v<V_{DC} < 1.68v$, $I_{DC}= -8,3.10^{-4} V_{DC}$
- Si $V_{DC} > 1.68v$, $I_{DC}= -5,1.10^{-4} V_{DC} - 5,5.10^{-4}$
On remarque que quel que soit la valeur de VDC : $$I_{DC}= f(V_{DC}) = (\frac{1}{R'}+ \frac{1}{R_4} + \frac{1}{R_5}) V_{DC} - \frac{1}{2}(\frac{1}{R_4} + \frac{1}{R_5}) (|V_{DC}+U_c|-|V_{DC}-U_c|)$$
Équations régissant l'oscillateur
Schéma équivalent
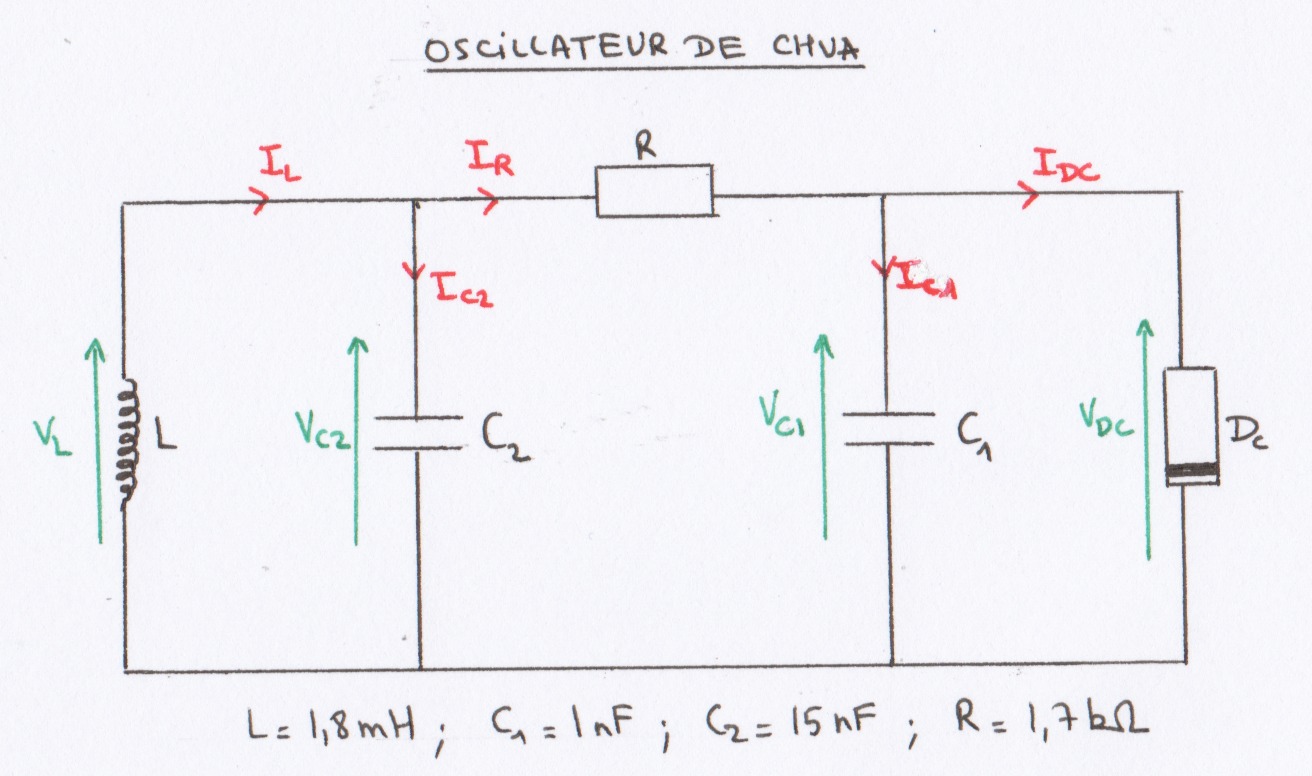
FIG 25 - Schéma équivalent de l'oscillateur de Chua
Loi des noeuds en B $I_R=I_{C_1}+I_{DC} \Rightarrow \frac{dV_{C_1}}{dt} = \frac{V_{C_2}-V_{C_1}}{R C_1} - \frac{f(V_{C_1})}{C_1}$
Loi des noeuds en A $I_L=I_{C_2}+I_R \Rightarrow \frac{dV_{C_2}}{dt} = \frac{I_L}{C_2}+\frac{V_{C_1}-V_{C_2}}{R C_2}$
Bobine $V_L = - L \frac{dI_L}{dt} \Rightarrow \frac{dI_L}{dt} = \frac{V_{C_2}}{L}$
On pose $x_1=\frac{V_{C_1}}{U_c}$, $x_2=\frac{V_{C_2}}{U_c}$, $x_3=\frac{RI_L}{U_c}$ et $t_c=\frac{t}{RC_2}$ pour adimensionner les équations. On obtient les équations : $$\frac{dx_1}{dt_c}=\frac{C_2}{C_1}(x_2-x_1-g(x_1))$$ $$\frac{dx_2}{dt_c}=x_1-x_2+x_3 $$ $$\frac{dx_3}{dt_c}=-C_2\frac{R^2}{L}x_2 $$ $$g(x_1)=\left(\frac{R}{R'}+ \frac{R}{R_4} + \frac{R}{R_5}\right) x_1 - \frac{1}{2}(\frac{R}{R_4} + \frac{R}{R_5})(|x_1+1|-|x_1-1|)$$
2.3 Résolution numérique des équations
Courbes en fonction du temps pour deux conditions initiales (1,1,0) et (1.01,1.01,0), ce qui représente une erreur relative de 1 %.
FIG 26 - Courbes temporelles de x1, x2 et x3. On remarque la sensibilité aux conditions initiales.
FIG 27 - Attracteur étrange : $x_2=f(x_1)$
2.4 Expérience et limites rencontrées
Montage
L'expérience est réalisée avec les composants cités précédemment, un oscilloscope et un ordinateur avec ORPHY.
FIG 28 - Montage
Caractéristique de la diode de Chua
$V_1=V_{DC}$ et $V_2=-R I_{DC}$ avec $R=1k\Omega$

FIG 29 - Caractéristique
Pour $-5v<V_2<5v$, on obtient la caractéristique théorique avec des valeurs de pente proches. En dehors de cette zone, les différences sont dues à l'approximation de la caractéristique des diodes $D_1$ et $D-2$ qui a plutôt l'allure d'une exponentielle croissante ainsi qu'à une saturation possible de l'amplificateur opérationnel : $|V_s|<V_{sat}=15v$.
Courbes de l'oscilloscope
FIG 30 - Caractéristique
FIG 31 - Attracteur étrange
On n'obtient pas un attracteur étrange, cela est certainement dû à la vitesse d'acquisition de l'oscilloscope.
Courbes temporelles
FIG 32 - Courbes temporelles de $x_1$ et $x_2$
On remarque bien que le système est apériodique. On peut donc en conclure qu'il est chaotique vu que l'on obtient les mêmes types de courbes que dans la théorie.
Attracteur étrange
FIG 33 - Attracteur étrange pour différentes valeurs de R.
Pour R<1480Ω, on obtient que l'oscillateur de Chua converge vers une position d'équilibre stable ($V_{C_1}$ et $V_{C_2}$ sont constants). Pour R>1480Ω, on obtient un attracteur étrange qui dépend de la valeur de R. Cette valeur limite est différente de la valeur théorique, cela est dû à l'imprécision sur les valeurs des résistances lors de l'expérience et au fait de la négligence de la résistance des fils et de la bobine.
On observe alors plusieurs fuseaux que l'on peut interpréter pour R=1840Ω. On retrouve alors l'attracteur étrange théorique en supposant que pour la caractéristique réelle des diodes, la saturation possible de l'amplificateur opérationnel et la valeur de R choisie, le passage d'une aile à l'autre se fait majoritairement par la périphérie.
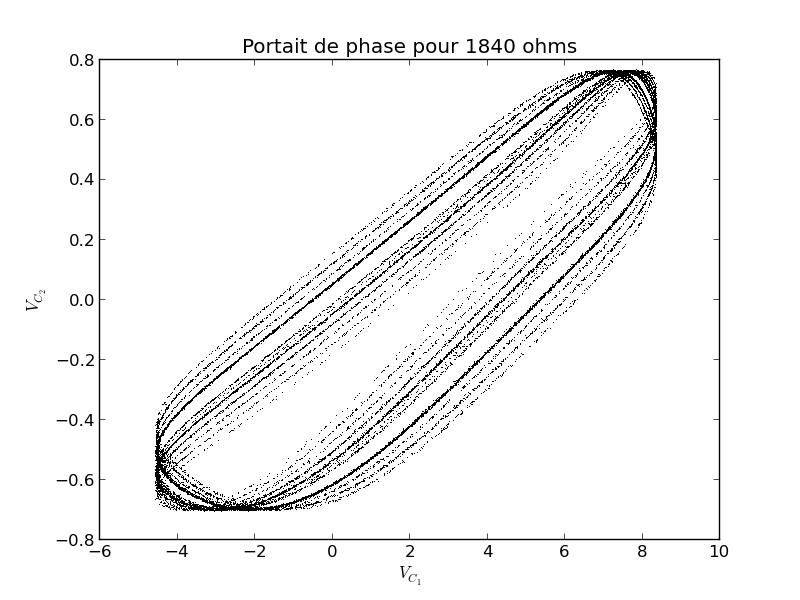
FIG 34 - Attracteur étrange pour R=1840Ω
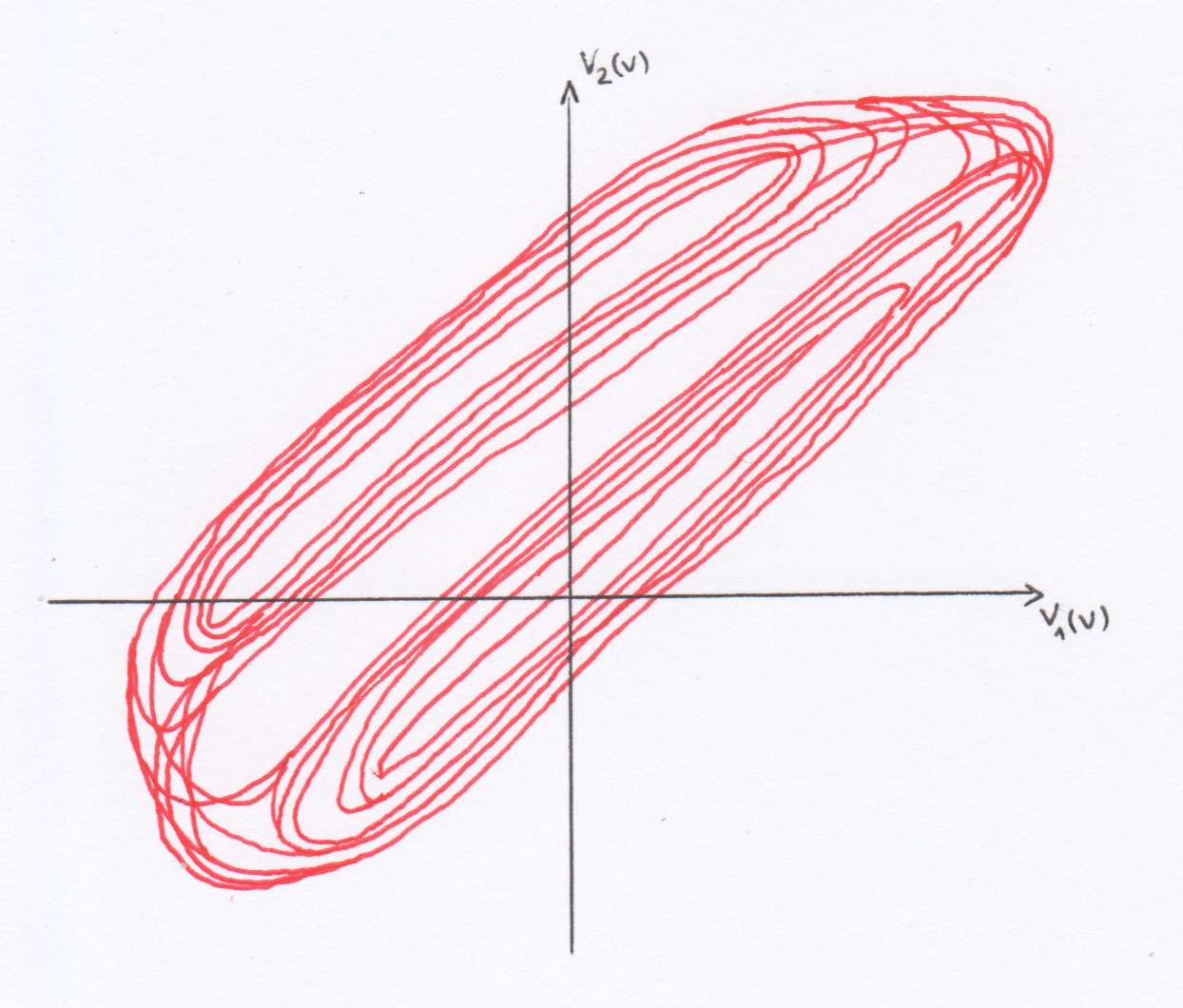
FIG 35 - Modélisation
3 Application à la convection de Rayleigh-Bénard
3.1 Position du problème
La convection de Rayleigh-Bénard est présente dans la vie de tous les jours : elle régit la dynamique des océans, de l'atmosphère, du magma au centre de la Terre mais aussi l'eau chauffée dans une casserole.
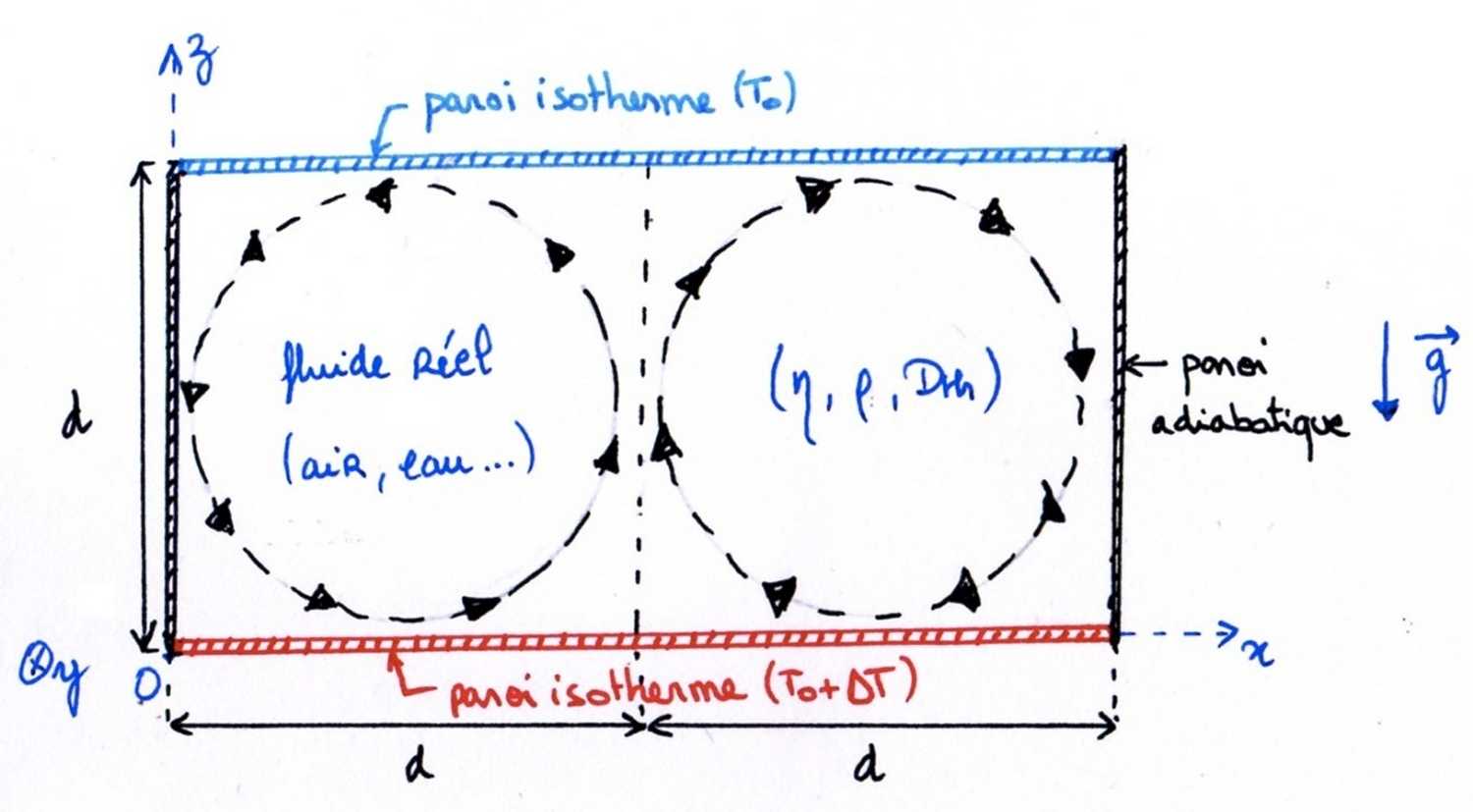
FIG 36 - Modèle de la convection de Rayleigh-Bénard
Soit $\Delta T \sim 100 K$ et $d \sim 1m$.
Le fluide en z=d est plus dense qu'en z=0. Donc deux phénomènes peuvent alors se produire : soit une diffusion thermique sans convection, le fluide est au repos, soit une diffusion thermique avec convection si $\Delta T > \Delta T_0$, on obtient alors des rouleaux convectifs. C'est ce phénomène qui sera étudié ici. Il a été étudié par Rayleigh en 1916 pour la première fois.
On considérera dans la suite que le fluide est de l'eau et le système d'étude est une particule de fluide.
3.2 Mise en mouvement
Temps caractéristique de la diffusion thermique $\tau_{th}$
D'après l'équation de diffusion $$\frac{DT}{Dt}=D_{th} \Delta T$$ on obtient $\tau_{th} \sim \frac{d^2}{D_{th}}$
Temps caractéristique du mouvement d'une particule de fluide $\tau_c$
D'après l'équation de Navier-Stokes, $$\rho \frac{D\vec v}{Dt} = - \vec \nabla P + \eta \vec \nabla ^2 \vec v + \rho \vec g$$ On considère que seules la pesanteur et la viscosité mettent en mouvement une particule de fluide : $\rho_0 \frac{v}{\tau_c} \sim \eta \frac{v}{d^2} - \Delta \rho g$.
D'où $\rho_0 \frac{d}{\tau_c^2} \sim \frac{\eta}{d \tau_c} - \Delta \rho g \Rightarrow \tau_c^2-\frac{\eta}{\Delta \rho g d} \tau_c \sim \frac{\rho_0 d}{\Delta \rho g}$
Donc on obtient $\tau_c \sim K \frac{\eta}{\Delta \rho g d}$ avec K une constante.
Relation entre ρ et T
Coefficient de dilatation volumique : $$\alpha = \left. -\frac{1}{\rho_0} \frac{\partial \rho}{\partial T}\right|_{P}$$
Coefficient de compressibilité isotherme : $$\chi_T = \left. \frac{1}{\rho_0} \frac{\partial \rho}{\partial P}\right|_{T}$$
D'où $d\rho=-\rho_0 \alpha dT + \rho_0 \chi_T dP$
Or pour l'eau, $\chi_T \Delta P \sim \chi_T \rho_0 g d \sim 5.10^{-6}$ et $\alpha \Delta T \sim 10^{-2}$ donc $d\rho = - \rho_0 \alpha dT$.
En intégrant, $\Delta \rho = - \rho_0 \alpha \Delta T$
D'où $\tau_c \sim K \frac{\eta}{\alpha \rho_0 d g \Delta T}$
Différents états possibles
Soit $$Ra=Gr.Pr=\frac{\alpha \rho_0 d^3 g}{\eta D_{th}} \Delta T = K\frac{\tau_{th}}{\tau_c}$$ le nombre de Rayleigh avec Pr le nombre de Prandtl (rapport en diffusivité de quantité de mouvement et diffusivité thermique) et Gr le nombre de Grashof (rapport entre forces de gravité et forces de viscosité). On appelle K le nombre de Rayleigh critique qui sépare le régime stationnaire du régime convectif. Il est de l'ordre de $10^3$.
- Si $\tau_{th}<\tau_c$ alors $Ra < K$ et $\Delta T < \Delta T_0$ : il n'y a pas de convection : la diffusion assure à elle seule le transfert thermique : la chaleur n'arrive pas à vaincre la viscosité du fluide pour le fluide en mouvement.
- Si $\tau_{th} \sim \tau_c$ alors $Ra \sim K$ : la particule de fluide est mise en mouvement car la diffusion thermique n'arrive plus à assurer le transfert thermique.
- Si $\tau_{th} > \tau_c$ alors $Ra>K$ et $\Delta T > \Delta T_0$ : La convection est prédominante. Elle se fait par rouleaux qui donne au fluide un mouvement de rotation uniforme.
- Si $\tau_{th} \gg \tau_c$ alors $Ra \gg K$ le mouvement devient instable à cause de la turbulence du fluide (nombre de Reynolds > 1000-2000) : il s'agit du régime chaotique. Dans ce cas, les rouleaux n'ont plus une vitesse uniforme, mais oscillent avec des inversions spontanées non prévisibles. Cela est dû au fait que les particules de fluides sont encore trop chaudes quand elles redescendent, ce qui provoque une remontée de ces particules à cause de leur densité et donc une inversion de rotation des rouleaux.
Analogie : la roue hydraulique de Lorenz
La roue hydraulique est une roue composée de seaux percés et d'une source d'eau venant du dessus (cf figure ci-dessous). Pour un petit débit volumique, les frottements de la roue ne sont pas vaincus par le remplissage du premier seau. Pour un grand débit volumique, la vitesse de la roue est constante et ne tourne que dans un sens (les seaux arrivent vides en bas). Pour un plus grand débit volumique, la roue oscille avec des inversions spontanées (régime chaotique) dues au fait que les seaux arrivent encore plein en bas.
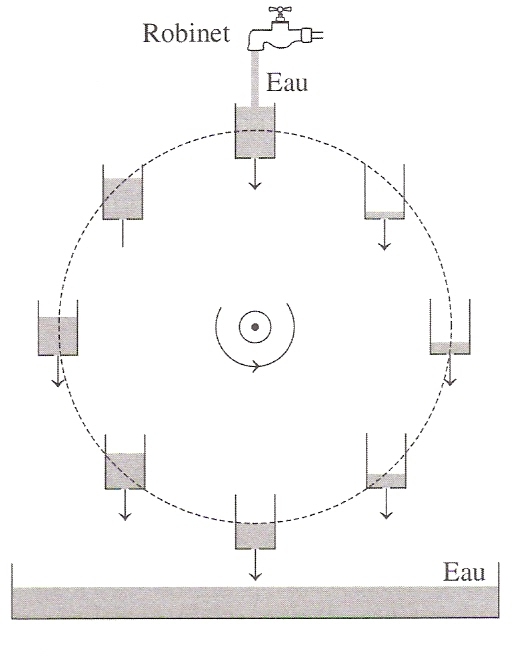
FIG 37 - Roue hydraulique de Lorenz
3.3 Mise en équation
Équations du mouvement
Le système est régit par trois équations non linéaire :
- L'équation de Navier-Stokes : $$\rho \frac{D\vec v}{Dt} = \rho \left(\frac{\partial \vec v}{\partial t} +(\vec v .\vec \nabla) \vec v\right)= - \vec \nabla P + \eta \vec \nabla ^2 \vec v + \rho \vec g$$
- L'équation de conservation de la masse : $$\frac{\partial \rho}{\partial t} + \vec \nabla .(\rho \vec v) = 0$$
- L'équation de diffusion thermique : $$\frac{DT}{Dt}=\frac{\partial T}{\partial t} +(\vec v .\vec \nabla) T=D_{th} \Delta T$$
On a obtenu à la section 3.2, $\rho = \rho_0 - \alpha \rho_0 (T-T_2)$. Dans l'approximation de Boussinesq, on n'en tiendra compte que dans le terme de gravité. Pour les autres termes, $\rho=\rho_0$.
Soient $\nu = \frac{\eta}{\rho_0}$ la viscosité cinématique du fluide, $P=p+\pi$ avec $\pi$ la pression hydrostatique et $\theta$ la perturbation de température par rapport au régime stationnaire. On obtient alors $$\theta(x,z,t)=T(x,z,t) + \frac{\Delta T}{d}(z-d) - T_0$$ On obtient alors le système ($\vec \nabla \pi = \rho_0 \vec g$) $$\rho_0 \left(\frac{\partial \vec v}{\partial t} +(\vec v .\vec \nabla) \vec v\right)= - \vec \nabla p + \rho_0 \alpha g \theta \vec e_z + \eta \vec \nabla ^2 \vec v \\ $$ $$\vec \nabla . \vec v =0 $$ $$\frac{\partial \theta}{\partial t} +(\vec v .\vec \nabla) \theta = \frac{\Delta T}{d} \vec v . \vec e_z + D_{th} \vec \nabla ^2 \theta$$
On adimensionne ces équations avec d pour les longueurs, $\tau_{th}=\frac{d^2}{D_{th}}$ pour le temps, $\frac{\Delta T}{Ra}$ pour $\theta$ et $\frac{\eta D_{th}}{d^2}$ pour p. On obtient alors le système (en grandeurs adimensionnées) : $$ \frac{D_{th}}{\nu} \left(\frac{\partial \vec v}{\partial t} +(\vec v .\vec \nabla) \vec v\right)= - \vec \nabla p + \theta \vec e_z + \vec \nabla ^2 \vec v $$ $$ \vec \nabla . \vec v =0 $$ $$\frac{\partial \theta}{\partial t} +(\vec v .\vec \nabla) \theta = Ra \vec v . \vec e_z + D_{th} \vec \nabla ^2 \theta$$
Mouvement dans le plan (xOz) : détermination de $\vec v$ et $\theta$
On se place alors dans le plan (xOz) où la particule de fluide a un mouvement plan sous forme de rouleaux. On a alors $\vec v (x,z,t)= u(x,z,t) \vec e_x + w(x,z,t) \vec e_z$. $$\frac{\partial u}{\partial x} + \frac{\partial w}{\partial z} = 0$$ On peut poser $\Psi$ de classe au moins $C_2$ telle que $$u=-\frac{\partial \Psi}{\partial z} \text{ et } w=\frac{\partial \Psi}{\partial x}$$
Conditions aux limites :
- aucun flux de matière à travers les surfaces en z=0 et z=1 : $w(z=0)=w(z=1)=0$
- aucune force de viscosité sur les surfaces dites libres en z'=0 et z'=1 : $\frac{\partial u}{\partial z}(z=0)=\frac{\partial u}{\partial z}(z=1)=0$
- Système de rouleaux suivant $\vec e_x$
On obtient alors $\Psi(z=0)=\Psi(z=1)=0$ et $\frac{\partial^2 \Psi}{\partial z^2}(z=0)=\frac{\partial^2 \Psi}{\partial z^2}(z=1)=0$. Donc $$\Psi(x,z,t)=\Psi_1(t) \sin(qx) \sin (\pi z)$$ on obtient alors les fonctions u et w.
en z'=0 et z'=1, la température est constante et égale à la température du régime stationnaire donc $\theta(z=0)=\theta(z=1)=0$. On pose alors $$\theta(x,z,t)=\theta_1(t) \cos(qx) \sin(\pi z)+ \theta_2(t) \sin(2 \pi z)$$ pour tenir compte de la dissymétrie des axes x et z en $\theta$.
Obtentions des équations de Lorenz
Les équations projetées de l'equation de Navier-Stokes respectivement sur l'axe 0x et Oz sont $$\frac{\partial}{\partial x} (1_z) - \frac{\partial}{\partial z} (1_x) \Rightarrow \frac{D_{th}}{\nu}\left(\frac{\partial \vec \nabla^2 \Psi}{\partial t} + \frac{\partial}{\partial x}(u\frac{\partial w}{\partial x}+w\frac{\partial w}{\partial z}) - \frac{\partial}{\partial z}(u\frac{\partial u}{\partial x}+w\frac{\partial u}{\partial z})\right) = \vec \nabla^4 \Psi + \frac{\partial \theta}{\partial x}$$ On remplace Ψ, u, v, et q on trouve alors : $$\frac{D_{th}}{\nu}\Psi_1'(t) +(\pi^2+q^2)\Psi_1(t)= \frac{q}{\pi^2+q^2}$$ L'équation de chaleur donne en regroupant les termes en $\sin(\pi z)$ et $\sin(2\pi z)$, $$\theta_1'(t)=-\pi q \Psi_1(t) \theta_2(t) + q Ra \Psi_1(t) - (\pi^2+q^2) \theta_1(t)$$ $$\theta_2'(t)=\frac{\pi}{2}q \Psi_1(t) \theta_1(t)-4\pi^2 \theta_2(t)$$
En posant, $$T=(\pi^2+q^2)t$$ $$X=\frac{\pi q}{\sqrt{2}(\pi^2+q^2)}\Psi_1$$ $$Y=\frac{\pi q^2}{\sqrt{2}(\pi^2+q^2)^3}\theta_1$$ $$Z=\frac{\pi q^2}{\sqrt{2}(\pi^2+q^2)^3}\theta_2$$ $$Pr=\frac{\nu}{D_{th}}$$ $$r=\frac{q^2}{(\pi^2+q^2)^3} Ra$$ $$b=\frac{4\pi^2}{\pi^2+q^2}$$ On retrouve les équations de Lorenz : $$\frac{dX}{dT}=Pr(Y-X)$$ $$\frac{dY}{dT}=-XZ+rX-Y$$ $$\frac{dZ}{dT}=XY-bZ$$
3.4 Résolution numérique
On prend Pr=10, b=8/3, r=28. Les courbes en fonction du temps sont représentées pour deux conditions initiales (10,10,10) et (10.1,10.1,10.1), ce qui représente une erreur relative de 1 % entre ces deux couples.
FIG 38 - Courbes temporelles de X, Y et Z
FIG 39 - Attracteur étrange
FIG 40 - Diagramme de bifurcation du point stationnaire $X_\infty = X(t \rightarrow \infty)$ en fonction du paramètre r. Pour 0 <r<1, $X_\infty=0$ est stable tandis que pour 1<r<24.74 $X_\infty=\sqrt{b(r-1)}$ est stable. La transition vers le chaos se produit à r=24.74 avec une bifurcation de Hopf, faisant apparaître un attracteur étrange. Cette bifurcation est sous-critique, ce qui permet de comprendre l'instabilité à r<24.74. Cette transition se réalise alors pour $q=0.5 \pi^2$ et $Ra = 16266$.
FIG 41 - Bifurcations unidimensionnelles [ajouter un paragraphe].
Conclusion
Cette étude sur les systèmes chaotiques permet de dire que le chaos touche beaucoup de domaines de la physique tels que la mécanique, l'électricité et la météorologie. Cependant, un système peut être à la fois chaotique et non chaotique suivant les paramètres qu'on lui impose (l'amplitude du couple donné au pendule, la résistance de l'oscillateur de Chua et la différence de température pour la convection de Rayleigh-Bénard). Pour des systèmes tels que l'atmosphère, cette différence de température ne peut pas être modifiée par l'homme, donc, en météorologie, la prévision ne pourra jamais se faire sur une très grande durée (supérieure à 1 mois). Il en est de même pour l'économie et la biologie. Pour des systèmes électriques et mécaniques, la valeur de ces paramètres peut être aisément changés donc si la prévision éternelle du circuit est voulue, elle peut être réalisée en adaptant la valeur de ces paramètres.
Bibliographie
Chaos
- http://eurserveur.insa-lyon.fr/approphys/9Math&Phys/Chaos/ (novembre 2011)
- http://www.edelo.net/chaos/sommaire.htm (novembre 2011)
- http://www.questmachine.org/article/La_théorie_du_chaos (décembre 2011)
- http://www.astrosurf.com/cieldaunis/chaos/index.html (décembre 2011)
- http://emmanuel.dauce.free.fr/sdsc/dau.html (décembre 2011)
- http://emmanuel.dauce.free.fr/these/node67.html (décembre 2011)
- http://chaos.pagesperso-orange.fr/intro.htm (décembre 2011)
- http://www.obs-nice.fr/etc7/utls/ (décembre 2011)
- http://vivienmallet.net/chaos/index.php (décembre 2011)
- http://just.loic.free.fr/index.php?page=accueil (décembre 2011)
- http://math.cmaisonneuve.qc.ca/alevesque/chaos_fract/chaos/chaos.html (décembre 2011)
- http://pascale.et.vincent.bourges.pagesperso-orange.fr/fractal/index.htm (2013)
- http://pascale.et.vincent.bourges.pagesperso-orange.fr/chaos/index.htm (2013)
Oscillateur de Chua
- http://lensors.ovh.org/fractals/index.php?page=diode (février 2012)
- http://www.chuacircuits.com/ (février 2012)
Lorenz
- http://hmf.enseeiht.fr/travaux/projnum/content/2011-g4/accueil (février 2012)
- http://bcev.nfrance.com/Lorenz/equations.htm (février 2012)
- http://images.math.cnrs.fr/Le-moulin-a-eau-de-Lorenz.html (novembre 2011)
- http://www.cax.free.fr/chaos/chaos.html (novembre 2011)
- http://just.loic.free.fr/index.php?page=accueil (2013)
Livre
- La théorie du chaos de James Gleick – Flammarion Champs sciences (1987-2008)
- Les lois du chaos d'Ilya Prigine – Flammarion Champs sciences (1993-2008)